Graph of 2x y 8 = 0 2x y 8 = 0 ⇒ y = (8 – 2x) (ii) Putting x = 1, we get y = 6 Putting x = 3, we get y = 2 Graphical Method of Solution of a Pair of Linear Equations video tutorial ; To have a graphic solution, You have identify a range of values for x That includes vertex and the above said two points Its vertex is given by x = −b 2 ×a = −3 2 ×1 = − 3 2 Now take four values above and below − 3 2 Find the corresponding y values for x Plot all the values Those coordinates where the curve cuts the xaxisDivide 0 0 by 4 4 Multiply − 1 1 by 0 0 Add − 8 8 and 0 0 Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e Set y y equal to the new right side Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k
The Substitution Method
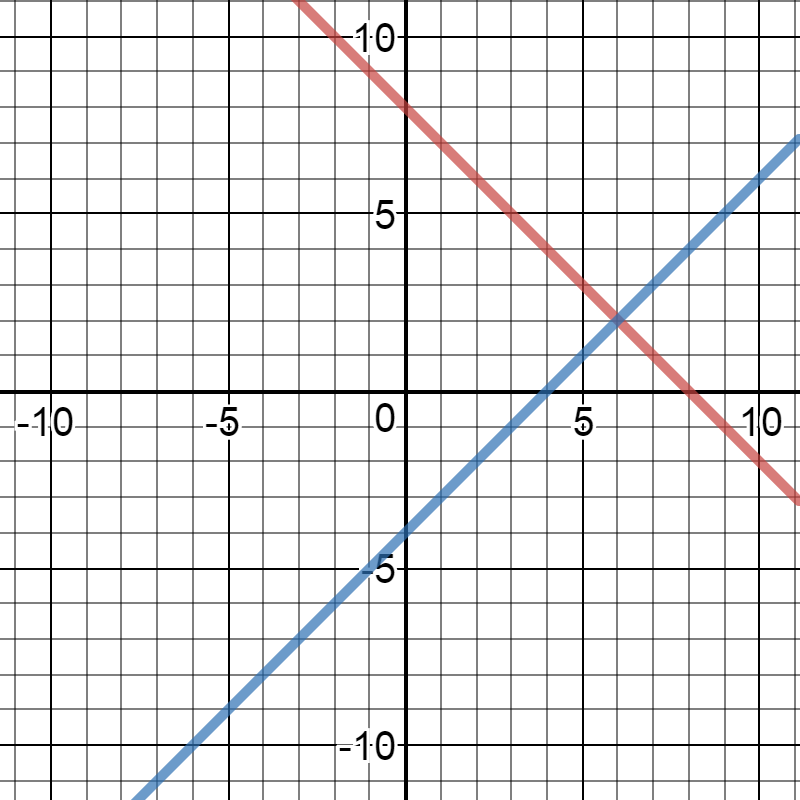
X+y=8 x-y=2 graphical method
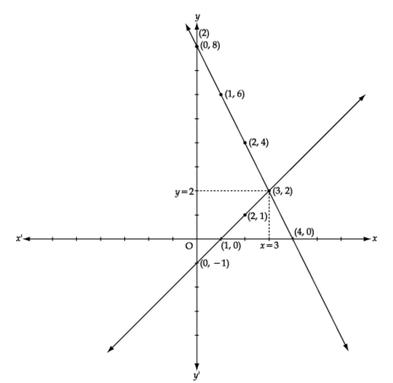
X+y=8 x-y=2 graphical method-Graphical Method of Solution of a Pair of Linear Equations video tutorial ;2 (x, y) (0, 8) (4, 0) (1, 6) (3, 2) The given lines intersect at (3, 2) ∴ x = 3 and y = 2 is the solution of the equations x – y = 1 and 2x y = 8 Concept Graphical Method of Solution of




Draw The Graphs Of The Equations X Y 1 And 2x Y 8 Shade The Area Bounded By These Two Lines And Y Axis Also Determine Maths Linear Equations In Two Variables Meritnation Com
Graphical Method of Solution of a Pair of Linear Equations video tutorial ;2x y 1 = 0 PDF FILE TO YOUR EMAIL IMMEDIATELY PURCHASE NOTES & PAPER SOLUTION @ Rs 50/ each (GST extra) HINDI ENTIRE PAPER SOLUTION MARATHI PAPER SOLUTION SSC MATHS ISolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
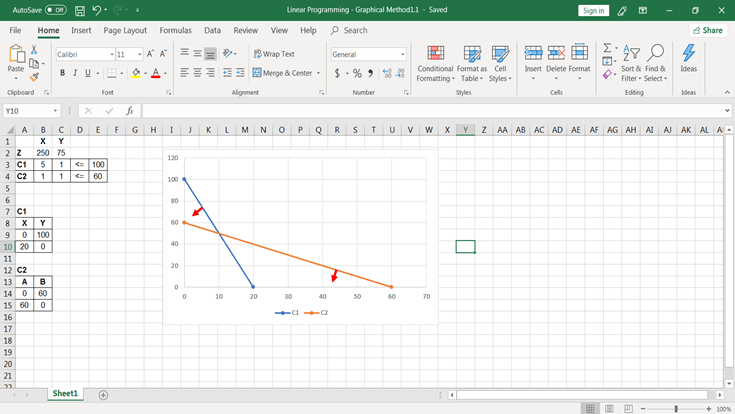
See the answer Find the optimal values of x and y using the graphical solution method Max 3xPreAlgebra Graph 2y=x 2y = x 2 y = x Divide each term by 2 2 and simplify Tap for more steps Divide each term in 2 y = x 2 y = x by 2 2 2 y 2 = x 2 2 y 2 = x 2 Cancel the common factor of 2 2 Tap for more stepsGraphical Method of Solution of a Pair of Linear Equations video tutorial
Graphical Method of Solution of a Pair of Linear Equations video tutorial ;Direction Opens Down Vertex (−1 2, 9 4) ( 1 2, 9 4) Focus (−1 2,2) ( 1 2, 2) Axis of Symmetry x = −1 2 x = 1 2 Directrix y = 5 2 y = 5 2 Select a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertexX y = 5 ಮತ್ತು 2x y = 8 ಸಮೀಕರಣಗಳನ್ನು ನಕ್ಷೆಯ ಸಹಾಯದಿಂದ ಬಿಡಿಸಿ



Linear Programming With Spreadsheets Datacamp



Solve X Y 1 And 2x Y 8 Graph Mathematics Topperlearning Com 4q3fx13uu
Graphical Method of solution of a pair of Linear Equations Solving equations the graphical way requires the equations to be plotted on the XY plane and then finding the solution Linear equation when plotted along the XY plane represents a straight line, as the degree of the equation is oneX y = 2 Then (x, y) is equal toSolve by Graphing xy=2 , xy=8, Subtract from both sides of the equation Multiply each term in by Tap for more steps Multiply each term in by Multiply Tap for more steps Multiply by Multiply by Simplify each term Tap for more steps Multiply by Multiply Tap for more steps
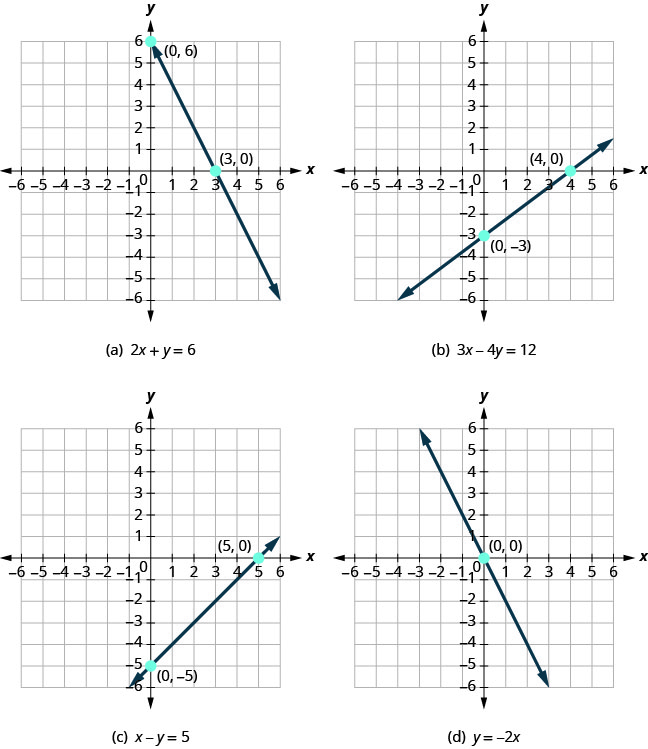



Graph With Intercepts Elementary Algebra




X Y 8 X Y 2 Graphical Method Novocom Top
Solve the pair of equations x 2 y = 9 and 2 x − y = 8 by graphical method Answer Solving simultaneous equations involves using algebra to eliminate one variable and solve for the other, then using that one to find the value of the otherSolve the following linear equation by substitution method xy=8 and xy=2 amanChauhan171 amanChauhan171 Math Secondary School Solve the following linear equation by substitution method xy=8 and xy=2 2 See answersDraw the first three constraints, which are lines You'll get a shape with straight sides (two of which are the x and yaxes) and a certain number of corners, one of which is (0,0) I didn't actually graph those particular lines, so I don't know




Graphing A Linear Equation 5x 2y Video Khan Academy



Graph Graph Equations With Step By Step Math Problem Solver
SOLUTION graph x y = 8 then make 8/1 = 8 The solution is x=6, y=2 See explanation below To solve such a system you should regard each equation as a function of x and y, where x_1y_1=8, or y_1=x_18 To be able to plot the graph you will note that x=0 gives y=8, and y=0 gives x=8, so the two points (0, 8) and (8, 0) are on the line x_2y_2=4, or y_2=x_24 x=0 gives y=4, and y=0 gives x= 4, so this line must go2x y = 9 Marathi



How Do You Solve The System Of Equations X Y 8 X Y 4 By Graphing Socratic



How To Solve X Y 7 And X Y 1 Graphically Quora
Solve the following system of equations by elimination method x y = 7xy;First of all develop an approach to the problem There can be two approaches * Simple analytical method of solving * Graphical method The above two equations are equations of 2nd degree And we know that to identify what a general 2nd order see below Graphically the roots are where the graph crosses the xaxis that is when y=0 graph{x^28x16 374, 1404, 256, 633} As can be seen from the graph it touches the xaxis at one point only x=4 Algebraically we could use factorising, completing the square or the formula look for factorising first x^28x=16=0 (x4)^2=(x4)(x4)=0 x4=0=>x=4 the



The Substitution Method



Solve The Following Systems Of Equations Graphically X Y 6 X Y 2 Sarthaks Econnect Largest Online Education Community
Graph x^2y^2=8 x2 y2 = 8 x 2 y 2 = 8 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h h represents the xoffset from theSolve the simultaneous equations by using Graphical method x 3y = 7;Example Using the graphical method, find the solution of the systems of equations y x = 3 y = 4x 2 Solution Draw the two lines graphically and determine the point of intersection from the graph From the graph, the point of intersection is (1, 2)




Draw The Graphs Of The Lines X Y 1 And 2x Y 8 Shade The Area Formed By Two Lines And The Y Axis Brainly In




Solving Simultaneous Equations Equations And Inequalities Siyavula
Using graphical method check whether the given equation is consistent 2 x 3 y = 8 and 3 x 6 y = 1 5 View solution Find graphically, the vertices of the triangle whose sides have the equations 2 y − x = 8 , 5 y − x = 1 4 and y − 2 x = 1View Solution X y 2 x 5 Use the graphical method Posted 4 months ago 6x = 3y 4x y = 1 Use the graphical method to solve each of the above pairs of equations Graphical Method Of Solving Linear Equations In Two Variables Let the system of pair of linear equations be a 1 x b 1 y = c 1 (1) a 2 x b 2 y = c 2 (2) We know that given two lines in a plane, only one of the following three possibilities can happen – (i) The two lines will intersect at one point
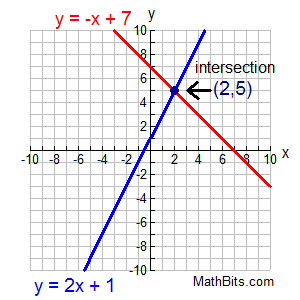



Systems Of Linear Equations Graphical Solution Mathbitsnotebook A1 Ccss Math




Solve The Pair Of Linear Equation Graphically X Y 1 2x Y 8 Also Find Coordinateof Vertices Of The Triangle Formed By The Lines And Maths Meritnation Com
Solved by pluggable solver Solve the System of Equations by Graphing Start with theFirst graph the three functions that result from ignore de inequalities, taking it as equalities * 3x4y=18 > y=18/43x/4 * x4y=16 > y=4x/4 * 3x2y=18 > y=93xThis video shows how to solve the following linear programming problem (involving multiple/alternative solutions) using graphical method~~~~~This chan




Graphical Method Of Solution Of A Pair Of Linear Equations Ck 12 Foundation




Solve Following Simultaneous Equation By Using Graphical Method X Y 8 X Y 2 Brainly In
Click here👆to get an answer to your question ️ Solve the following pair of linear equations using Graphical method x y = 8; Refer explanation METHOD 1 ALGEBRA y =x^22x8 is quadratic in x a=1,b=2,c=8 As coefficient of x^2 is positive so, its graph will be mouth opening upward parabola Check discriminant of the quadratic to examine the nature of the roots D=b^24ac D=432=36 As D>0, the roots of quadratic will be real and unequal Also, we can find roots of y=0 that are x=4,2 Here, y=8 at xGraphical Method of Solution of a Pair of Linear Equations video tutorial ;



If X Y 3 X Y 1 Then What Is X Y Quora




Graph Graph Inequalities With Step By Step Math Problem Solver
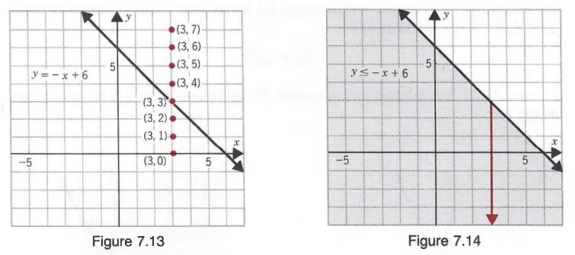
Math 1313 Page 6 of 19 Section 21 Example 4 Use the graphical method to solve the following linear programming problem Maximize R x y= 4 11 subject to 3 2 4 0 0 x y x y x y ≤ ≤ ≥ ≥ Solution We need to graph the system of inequalities to produce the feasible set We will start See a solution process below First, we can graph the first line by find two points on the line, plotting them and drawing a line through them For x = 0 0 y = 2 y = 2 color(red)(1) xx y = color(red)(1) xx 2 y = 2 or (0, 2) For y = 0 x 0 = 2 x = 2 or (2, 0) graph{(x^2(y2)^125)((x2)^2y^125)(xy2)=0 ,,10,10} We can now do the same thing for the Transcript Example 15 Solve the following system of inequalities graphically x 2y ≤ 8 , 2x y ≤ 8 , x ≥ 0 , y ≥ 0 First we solve x 2y ≤ 8 Lets first draw graph of x 2y = 8 Putting x = 0 in (1) 0 2y = 8 2y = 8 y = 8/2 y = 4 Putting y = 0 in (1) x 2(0) = 8 x 0 = 8 x = 8 Points to be plotted are (0,4) , (8,0) Drawing graph Checking for (0,0) Putting x = 0, y = 0 x 2y ≤
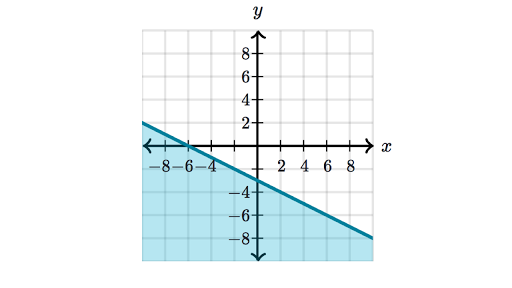



Graphing Inequalities X Y Plane Review Article Khan Academy




Solve 2x Y 5 And 3x 2y 8
Find the graphical solution of the inequality 10x4y 8 2 Find the graphical solution of the inequality 2x5y>10 3 Write a system of linear inequalities that describes the shaded region xy 5 2xy 8 2xy 1 x 0 y 0 4 Fall 17, Maya Johnson The Method of Corners 1 Graph the feasible set 2 If the feasible set is nonempty, findUse graphical methods to solve the linear programming problem Maximize z = 6x 7y subject to 2x 3y ≤ 12 2x y ≤ 8 x ≥ 0 y ≥ 0 A) Maximum of 24 when x = 4 and y = 0 B) Maximum of 32 when x = 2 and y = 3 C) Maximum of 32 when x = 3 and y = 2 D) Maximum of 52 when x = 4 and y = 4 Answer by jim_thompson5910() (Show Source)View Math1mod7pdf from ECON 1 at Institute of Chartered Secretaries and Administrators Mathematics 1 Module VII Lesson 1 LINEAR EQUATIONS Lesson Objectives At the end of the lesson, you should be
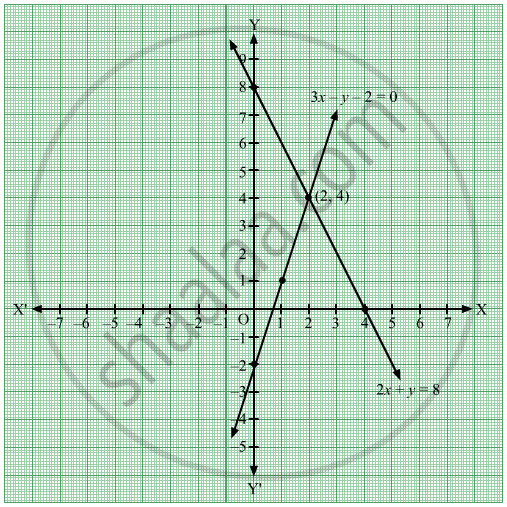



Solve The Following Simultaneous Equation Graphically 3x Y 2 0 2x Y 8 Algebra Shaalaa Com



Graph Graph Inequalities With Step By Step Math Problem Solver
Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepQuestion Find The Optimal Values Of X And Y Using The Graphical Solution Method Max 3x 2y Subject To X ≤ 6 X Y ≤ 8 2x Y ≥ 8 2x 3y ≥ 12 X ≥ 0, Y ≥ 0 This problem has been solved!See the answer Find the optimal values of x and y using the graphical solution method Max 3x 2y subject to x 6 x y 8 2x y 8 2x 3y 12 x 0, y 0
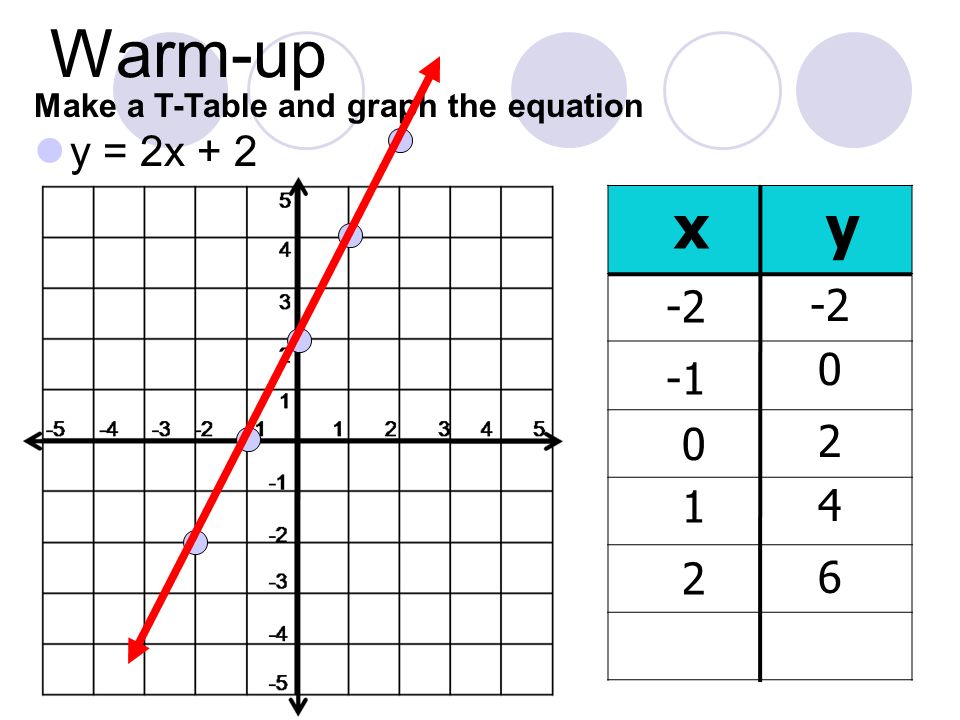



Warm Up Make A T Table And Graph The Equation Y 2x 2 X Y Ppt Video Online Download
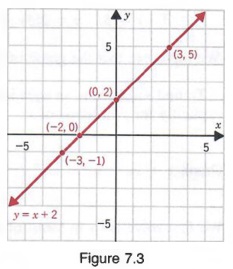



Graph Graph Equations With Step By Step Math Problem Solver
Observe that, given any values for x3 and x4, the values of x1 and x2 are determined uniquely by the equalities In fact, setting x3 = x4 = 0 immediately gives a feasible solution with x1 = 6 and x2 = 4 Solutions such as these will play a central role in the simplex method and are referred to as basic feasible solutionsX, y={8, 2} PREMISES The values of x and y if (xy, xy)={6, 10} ASSUMPTIONS Let (xy=6) and (xy=10) represent a system of two equations that can be used to solveThis problem has been solved!




Draw Graph For X Y 5 X Y 8 Brainly In




Q3d 3x Y 2 0 2x Y 8 Solve The Following Simultaneous Equation Graphically
Question xy=8;xy=2 simeltenious equations using graphical method Answer by MathLover1() (Show Source) You can put this solution on YOUR website!Subtract y from both sides x^ {2}2xy8=0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x=\frac {2±\sqrt {2^ {2}4\left (y8\right)}} {2}Solve the System of Equation Graphically 2x 3y = 2, X – 2y = 8




3nsrmmffkem Xm
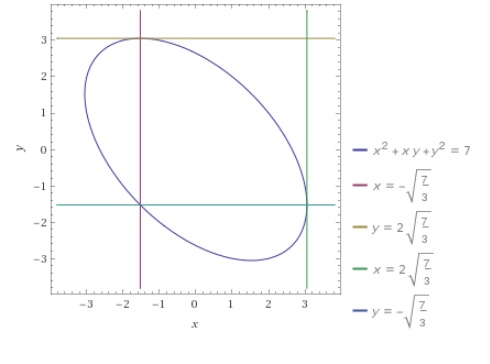



How Do You Find All Points On The Curve X 2 Xy Y 2 7 Where The Tangent Line Is Parallel To The X Axis And The Point Where The Tangent Line
Ex 63, 12 Solve the following system of inequalities graphically x – 2y ≤ 3, 3x 4y ≥ 12, x ≥ 0, y ≥ 1 First we solve x – 2y ≥ 3 Lets first draw graph of x – 2y = 3 Putting x = 0 in (1) 0 – 2y = 3 −2y = 3 y = ( 3)/ ( −2) y = –15 Putting y = 0 in (1) x – 2 (0) = 3 x – 0 = 3 x = 3 Drawing graph Checking for (0,0#SahajAdhyayan #सहजअध्ययन #graphically Class 10 (इयत्ता 10वी ) Practice set 12 (सराव संच 12) Graphical Method x y = 0 ;Putting x = 4, we get y = 5 Thus, we have the following table for the equation 3x 2y – 2 = 0 Now, plot the points P (0, 1) and Q (4, 5) The point C (2, 2) has already been plotted Join PC and QC and extend it on both ways Thus, PQ is the graph of 3x 2y – 2 = 0 The two graph lines intersect at A (2, 2)
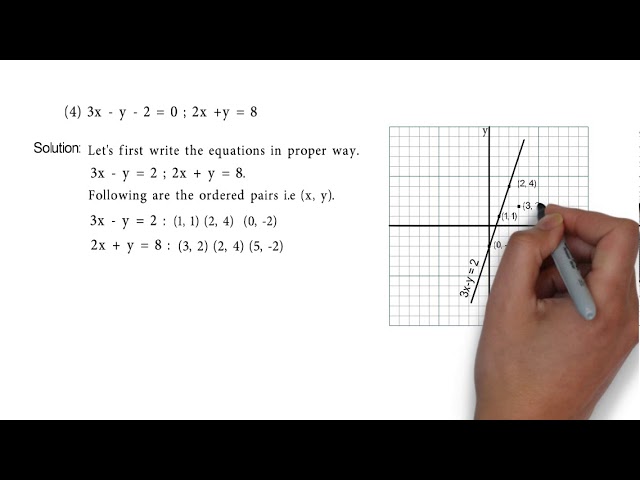



3x Y 2 0 And 2x Y 8 Problem Set 1 Q3 4 Of Linear Equations In Two Variables Algebra Youtube
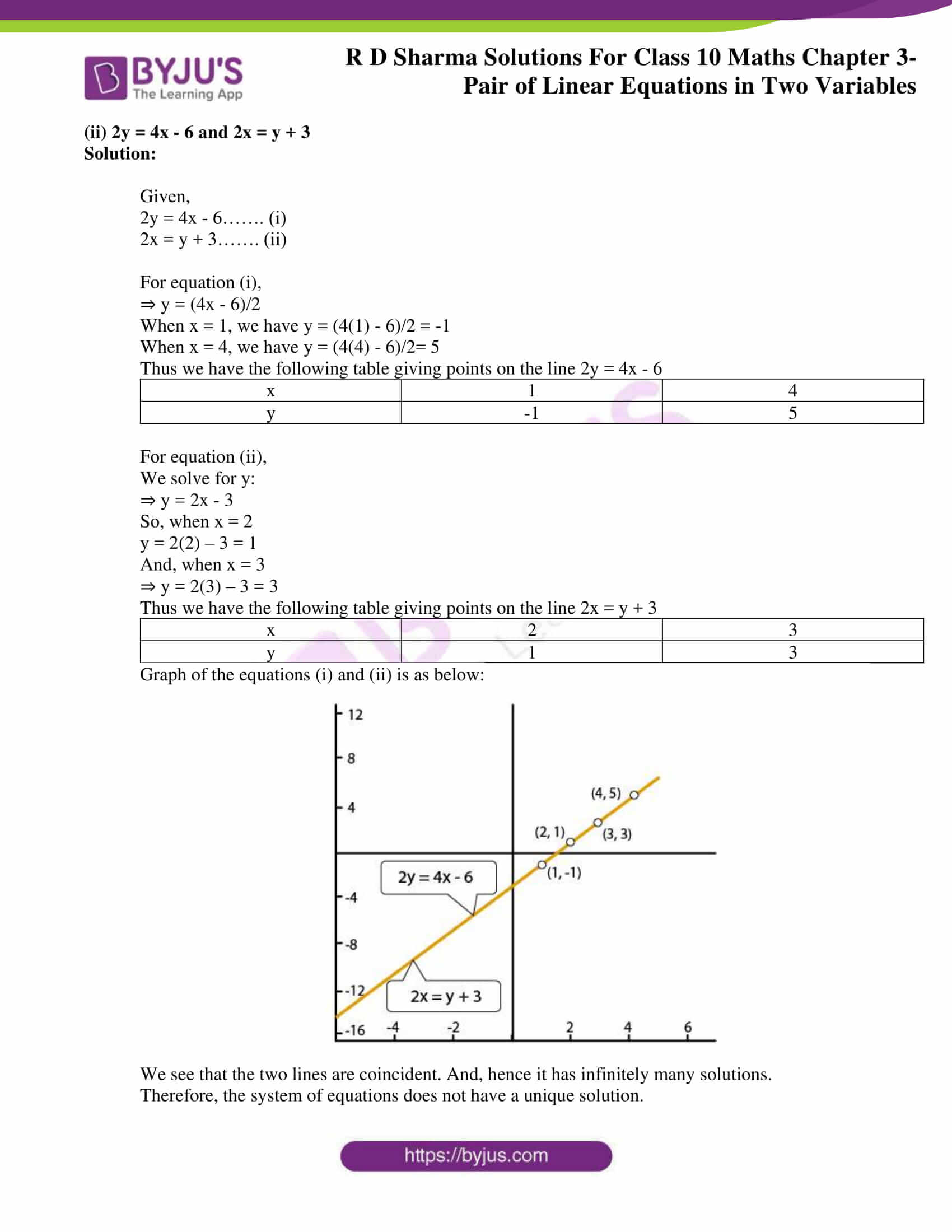



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2
The graphical solution of the simultaneous equations is given by the point of intersection of the linear equations Consider x y = 8 xintercept When y = 0, x = 8 yintercept When x = 0, y = 8 Consider x – y = 2 xintercept When y = 0, x = 2 yintercept The diagram shows that the lines intersect at the point (5, 3) So, the2x – 3y = – xy asked in Linear Equations by Anika01 ( 571k points) pair of linear equations in two variablesCompare the algebraic method and the graphical method for solving a linear equation with variables on both sides Describe the advantages and disadvantages of each method USING TOOLS x − 2 = −4x 3 x y 2 4 −4 −2 1 2 4 x −2 −4 −6 In




Draw The Graph Of The Equation X Y 3 And Y X 1 What Do You
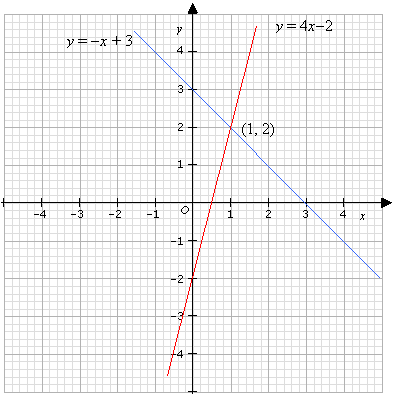



Systems Of Equations Graphical Method Video Lessons Examples Solutions




Ex 6 3 8 Solve X Y 9 Y X X 0 Graphically Ex 6 3




Graphical Method Of Solving Linear Equations In Two Variables A Plus Topper




Ex 6 2 5 Solve X Y 2 Graphically Chapter 6 Cbse




Ex 6 2 5 Solve X Y 2 Graphically Chapter 6 Cbse




2 X Y 3 X Y 1 8 X Y 7 X Y 5 6 Solve X And Y Youtube
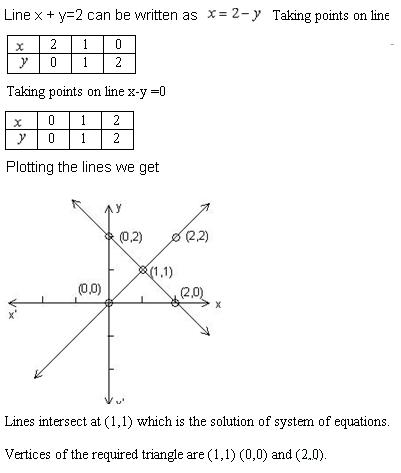



Draw The Graph Of X Y 2 And X Y 0 And Hence Find The Vertices Of The Triangle Formed By The Lines And The X Axis Mathematics Topperlearning Com Sljoqnfee
.jpg)



Solve The Following Simullanwous Equations Using Graphical Methods X Y 8 X Y 2 Maths Meritnation Com




Graphing Inequalities X Y Plane Review Article Khan Academy



3 Graphical Solution Of A System Of Linear Equations



1




Ex 6 3 7 Solve 2x Y 8 X 2y 10 Graphically Ex 6 3




X Y 8 X Y 2 Solution Of This Sum In Graphical Method Brainly In
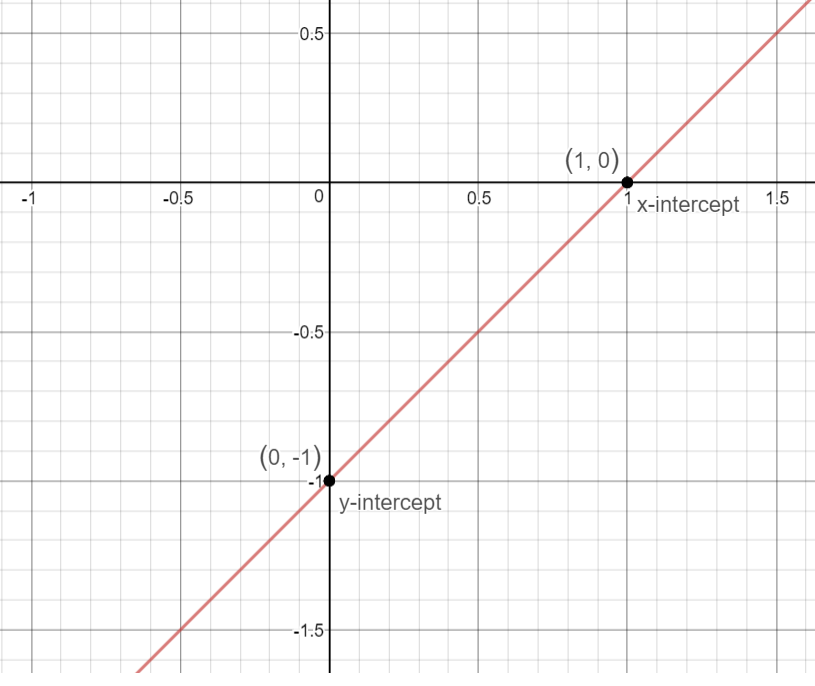



How Do You Graph X Y 1 Socratic



What Is The Graph Of Xy 2 Quora




2x Y 8 X Y 1 Solve Graphically Brainly In



Solve The Following Simultaneous Equations Graphically




Solve The Following Two Linear Equations Graphically X Y 8 3x 3y 16 Brainly In




Draw The Graphs Of The Equations X Y 1 And 2x Y 8 Shade The Area Bounded By These Two Lines And Y Axis Also Determine Maths Linear Equations In Two Variables Meritnation Com



16 X Y 2 X Y 1 8 X Y 12 X Y 7 Find The Value Of X And Y Quora



The Substitution Method
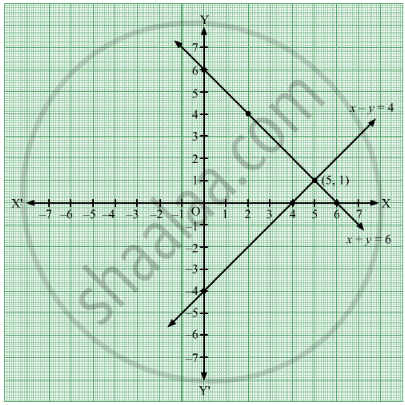



Solve The Following Simultaneous Equations Graphically X Y 6 X Y 4 Algebra Shaalaa Com
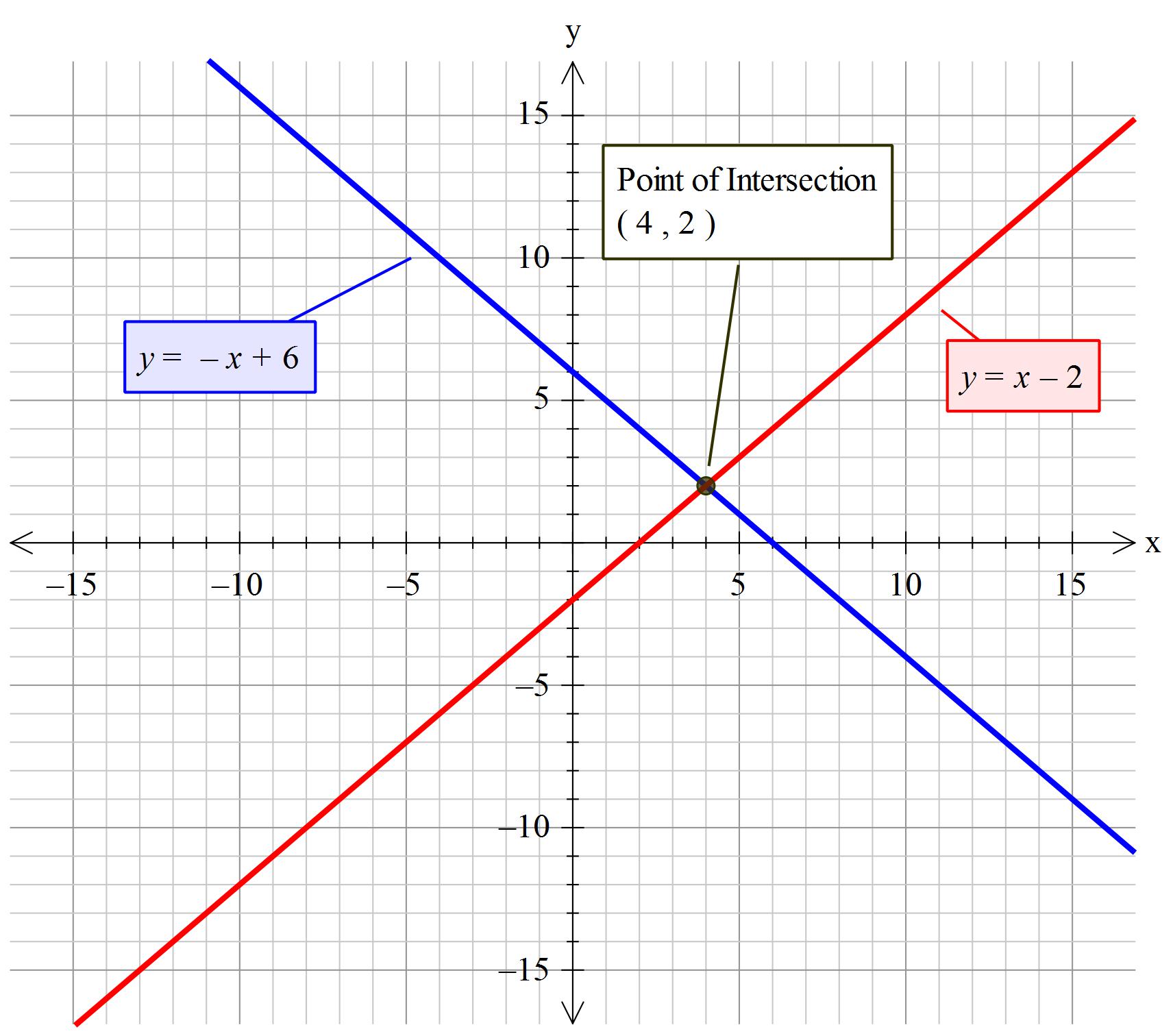



How Do You Solve The System X Y 6 And X Y 2 By Graphing Socratic




Draw The Graphs Of The Equations X Y 1 A N D 2x Y 8 Shade The




Graphical Method Of Solving Linear Equations In Two Variables A Plus Topper
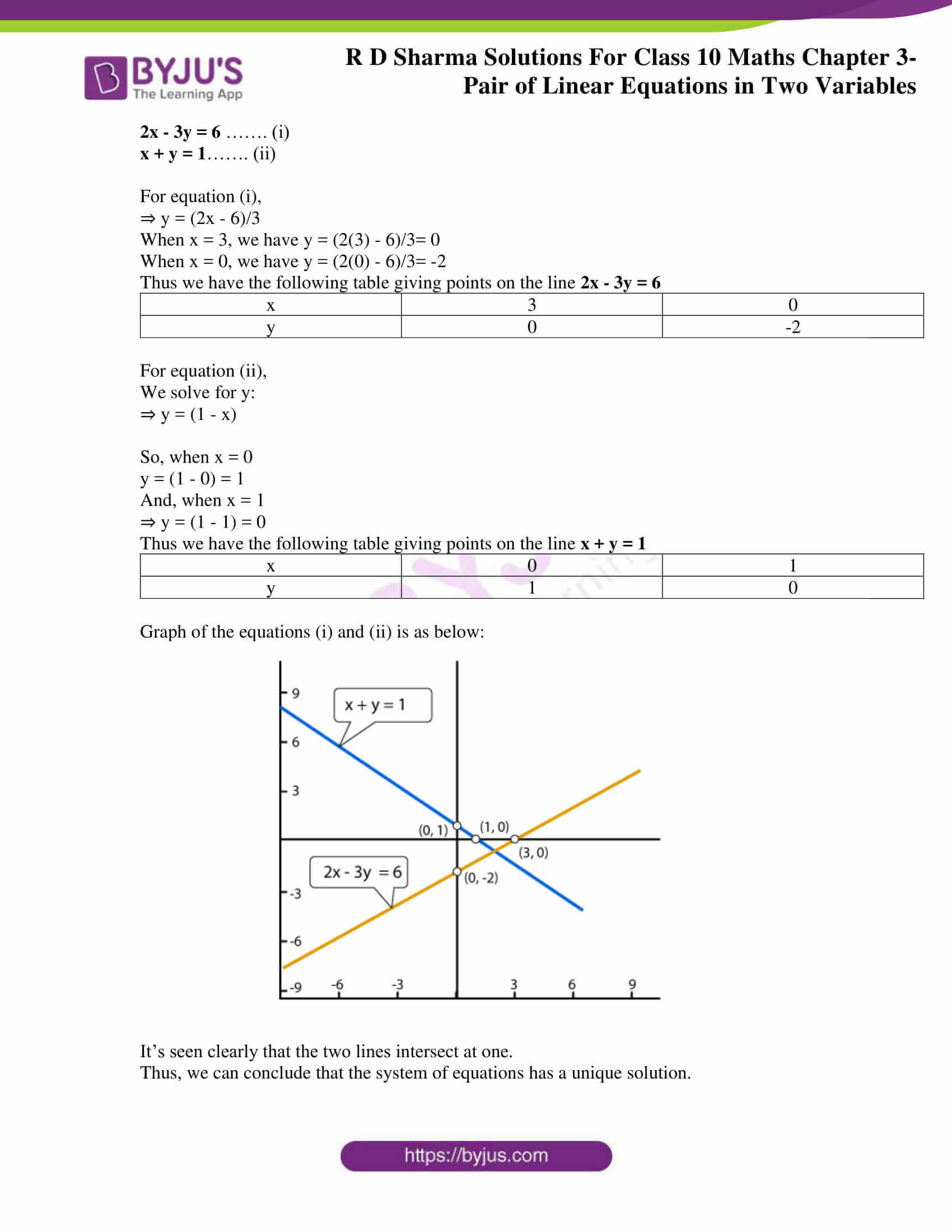



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2




Draw The Graphs Of The Lines X Y 1 And 2x Y 8 Shaded The Areas Formed By These Two Lines And The Y Axis Also Find This Area




Solving Simultaneous Equations Equations And Inequalities Siyavula



Final Exam Lars Hondorf



Solve The Following Systems Of Equations Graphically X Y 6 X Y 2 Sarthaks Econnect Largest Online Education Community



1




Solve Graphically X Y 8 X Y 2 Novocom Top
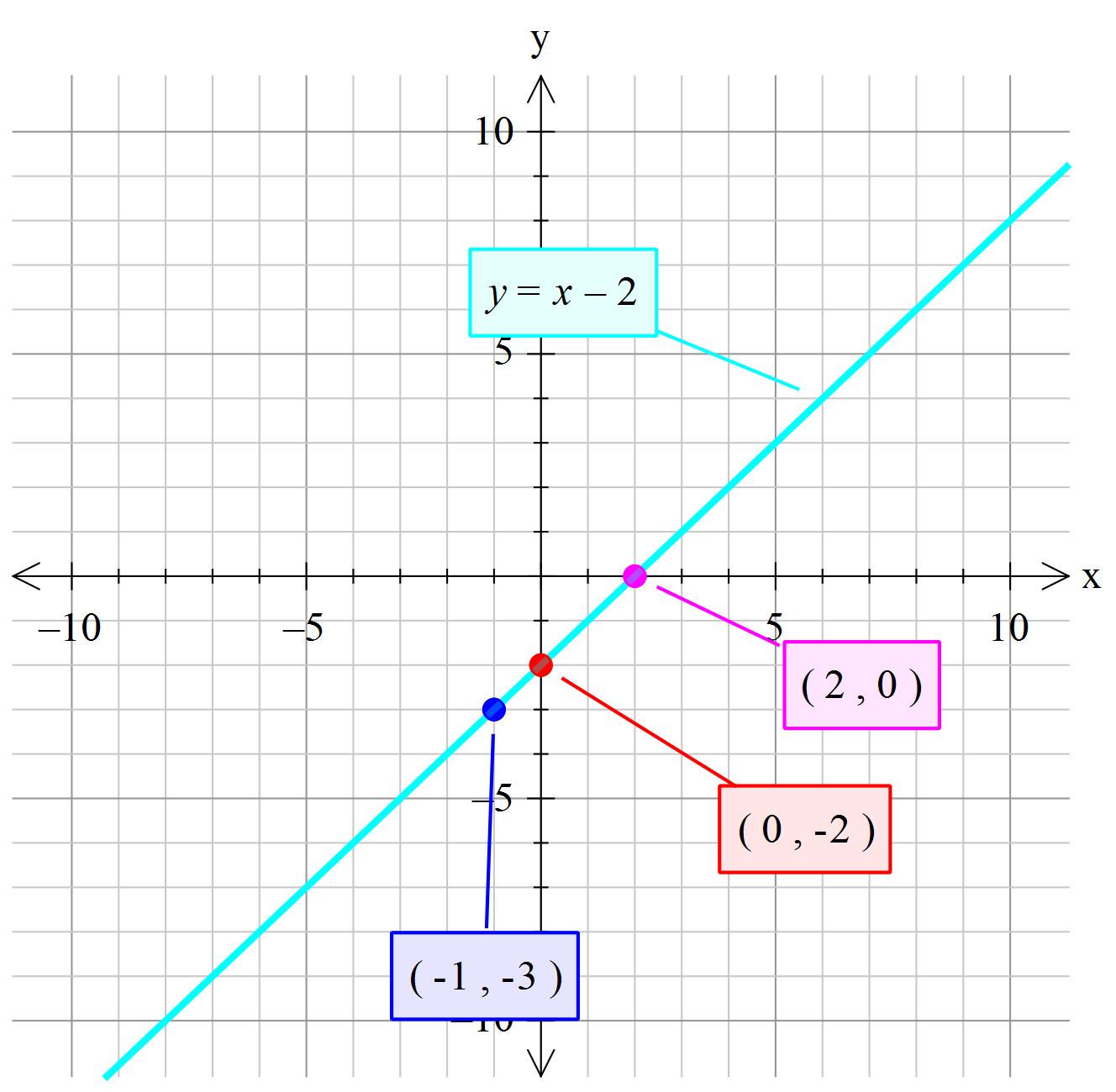



How Do You Graph The Line X Y 2 Socratic
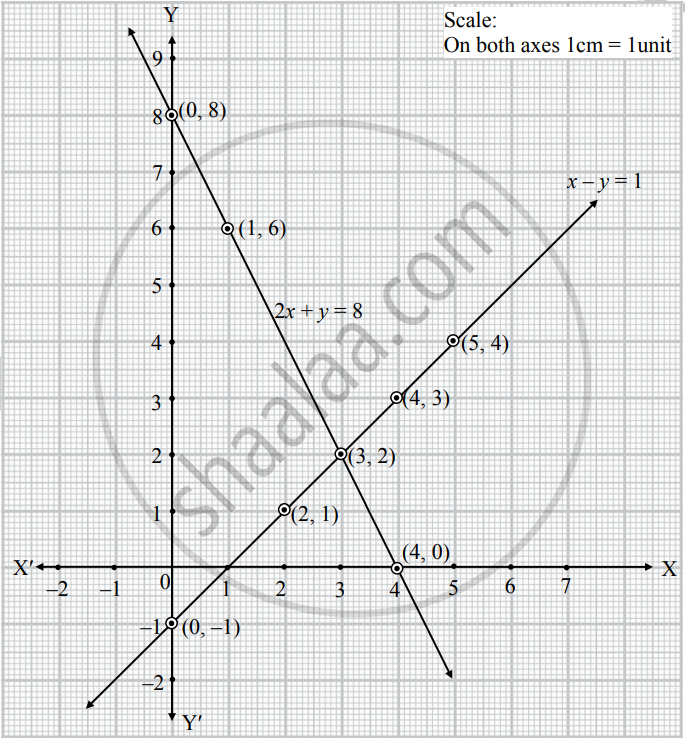



Solve The Following Equations By Graphical Method X Y 1 2x Y 8 Algebra Shaalaa Com



16 X Y 2 X Y 1 8 X Y 12 X Y 7 Find The Value Of X And Y Quora
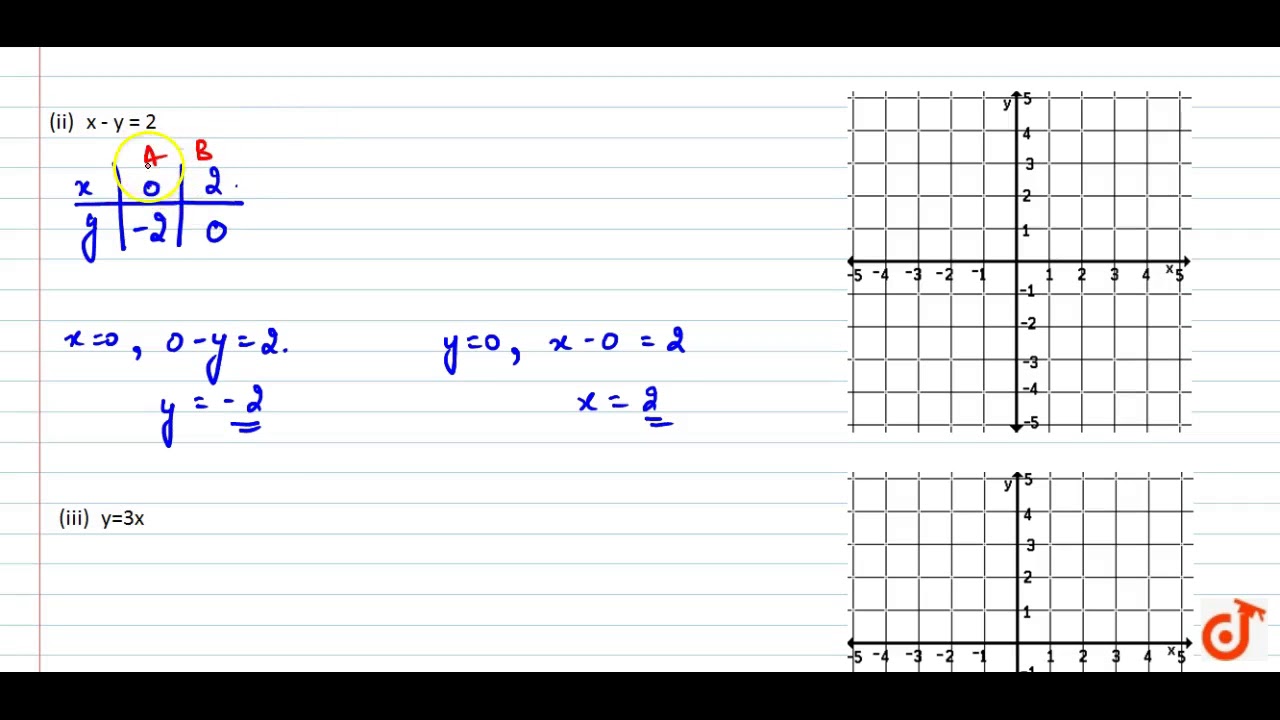



Draw The Graph Of Each Of The Following Linear Equations In Two Variables I X Y 4 Ii X Y Youtube



1
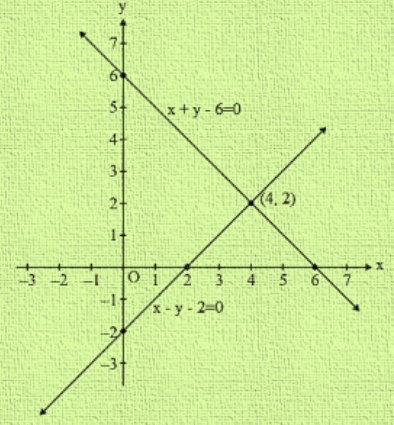



R D Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2



How Do You Solve The System Of Equations X Y 8 X Y 4 By Graphing Socratic




Solve The Following Simultaneous Equations Using Graphical Method X Y 8 X Y 2



What Is The Graph Of Xy 2 Quora
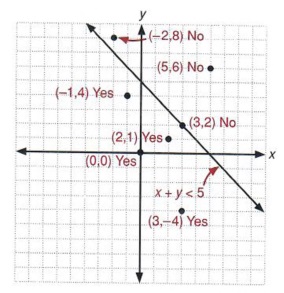



Graph Graph Inequalities With Step By Step Math Problem Solver




2x Y 11 And X Y 8 Solve Using Substitution And Elimination Method Youtube




Graphically Solve The Following Pair Of Equations 2x Y 6 And 2x Y 2 0 Find The Ratio Of The Areas Youtube



Q Tbn And9gctwl8ksal48ks9fvcggchq7ifw Mt5nzxx1 0ivsjobxia io Usqp Cau
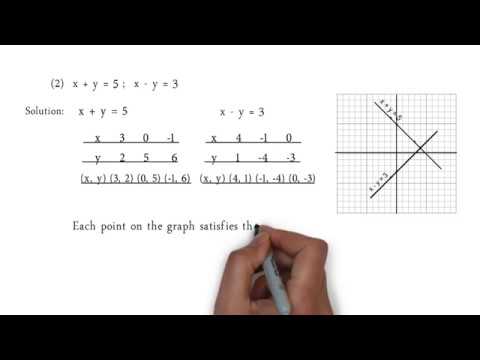



X Y 5 And X Y 3 P S 1 2 Q2 2 Linear Equations In Two Variables Youtube




Example 15 Chapter 6 Solve X 2y 8 2x Y 8



What Is The Graph Of Xy 2 Quora




Implicit Differentiation




Solve The Following Two Linear Equations Graphically X Y 8 3x 3y 16 Brainly In




Graphical Method Of Solution Of A Pair Of Linear Equations Ck 12 Foundation



X Y 2 Graph The Linear Equation Mathskey Com




Solve The Problem Of An Equation Graphically X Y 5 X Y 8 Brainly In




Draw The Graphs Of The Pair Of Linear Equations X Y 2 0 Amp 4x Y 4 0 Determine The Co Ordinates Of The Vertices Of The Triangle Formed By The Lines



Solution X Y 8 X Y 2 Simeltenious Equations Using Graphical Method



Solve The Following Simultaneous Equations Graphically I 3x Y 2 0 2x Y 8 Ii 3x Y 10 X Y 2 Sarthaks Econnect Largest Online Education Community
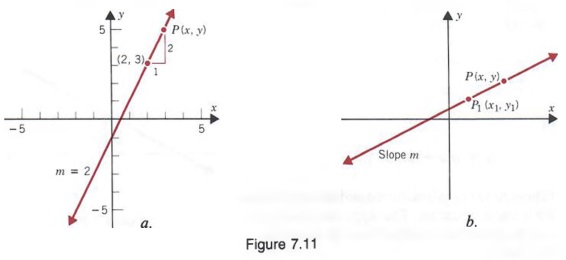



Graph Graph Equations With Step By Step Math Problem Solver




Solve Pair Of Linear Equations Graphically 2x Y 8 2x Y 4 Brainly In




Example 15 Chapter 6 Solve X 2y 8 2x Y 8




Solving Simultaneous Equations Equations And Inequalities Siyavula



Graph Graph Equations With Step By Step Math Problem Solver




Graphical Method Of Solving Linear Equations In Two Variables A Plus Topper



Solve The Following System Of Linear Equations Graphically X Y 1 2x Y 8 Mathematics Topperlearning Com D18z0rl11




Omtex Classes X Y 8 X Y 2
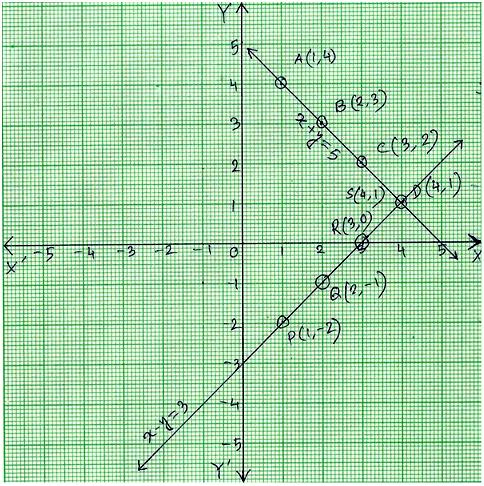



Simultaneous Equations Graphically Solve Graphically The System Of Equations




Solve X Y 7 And 3x 2y 11




Solve The Following Pair Of Linear Equations Using Graphical Method X Y 8 X Y 2 Then X Y Is Equal To
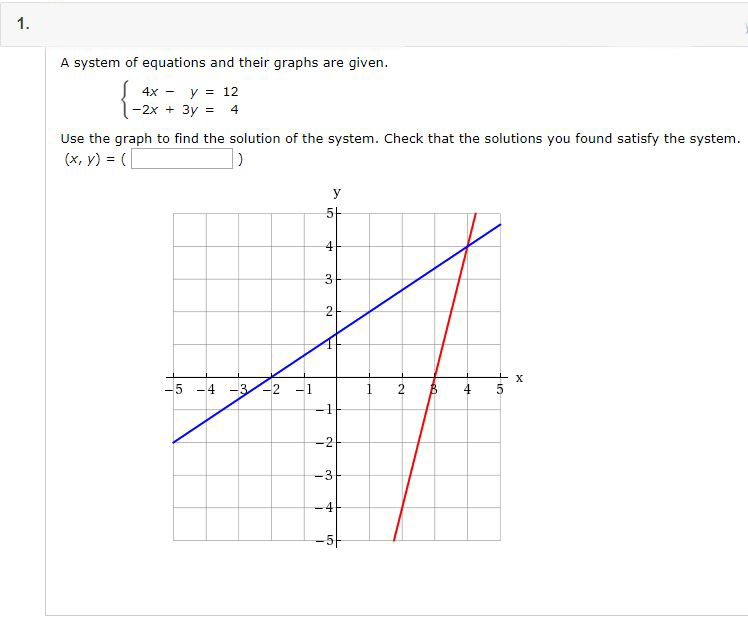



A System Of Equations And Their Graphs Are Given 4x Chegg Com



Systems Of Linear Equations




Solve The Equations Using Graphical Method X Y 3 And 3x 2y 1




Graphical Method Of Solution Of A Pair Of Linear Equations Ck 12 Foundation
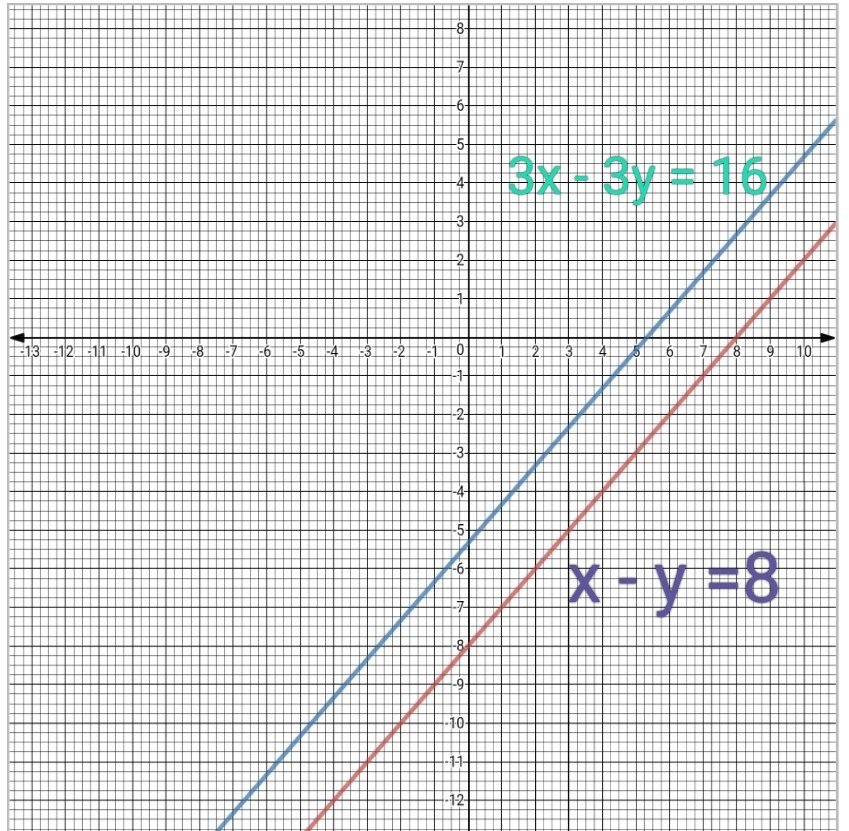



Show Graphically That The System Of Linear Equations X Y 8 3x 3y 16 Is Inconsistent I E It Has No Solution Snapsolve
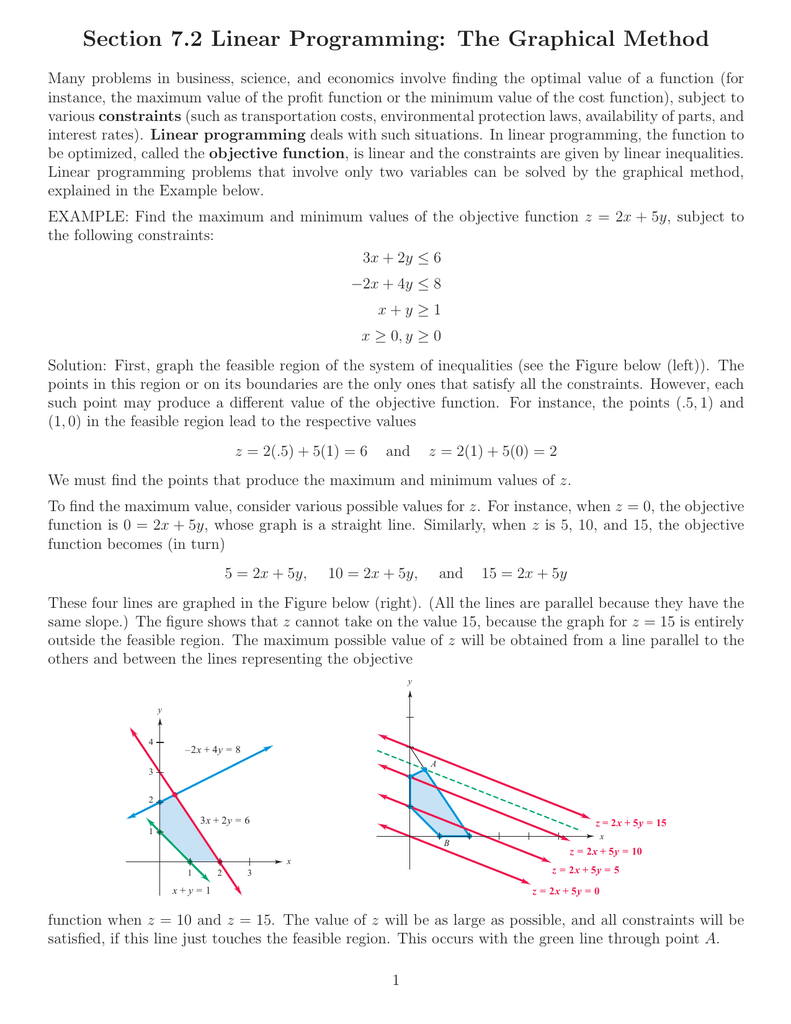



Section 7 2 Linear Programming The Graphical Method


