In this video, you will learn how to do a reflection over the line y = x The line y=x, when graphed on a graphing calculator, would appear as a straight line cutting through the origin with a slope of 1 For triangle ABC with coordinate points A (3,3), B (2,1), and C (6,2), apply a reflection over the line$\endgroup$ – user Jan 15 '17 at 805 $\begingroup$ RightThe line given is `5xy6=0` and the point is (4,13) Let the reflection be (a,b), then the midpoint of (4,13) and (a,b) lies on the given curve

Reflecting Shapes Article Reflections Khan Academy
Reflection on line x+y=6
Reflection on line x+y=6- Given that the line passes through (1, 2, 4) and this point also lies on the given plane Thus, required line will be in the form of (x 1)/l = (y 2)/m = (z 4)/n Any point on the given line is (r 1 1, 3r 1 2, r 1 4) If r 1 = 1, this point becomes P = (0, 5, 5) Let Q = (a, b, c) be the reflection of 'P' in the given plane ThenFree graphing calculator instantly graphs your math problems



3d Reflection In Computer Graphics Definition Examples Gate Vidyalay
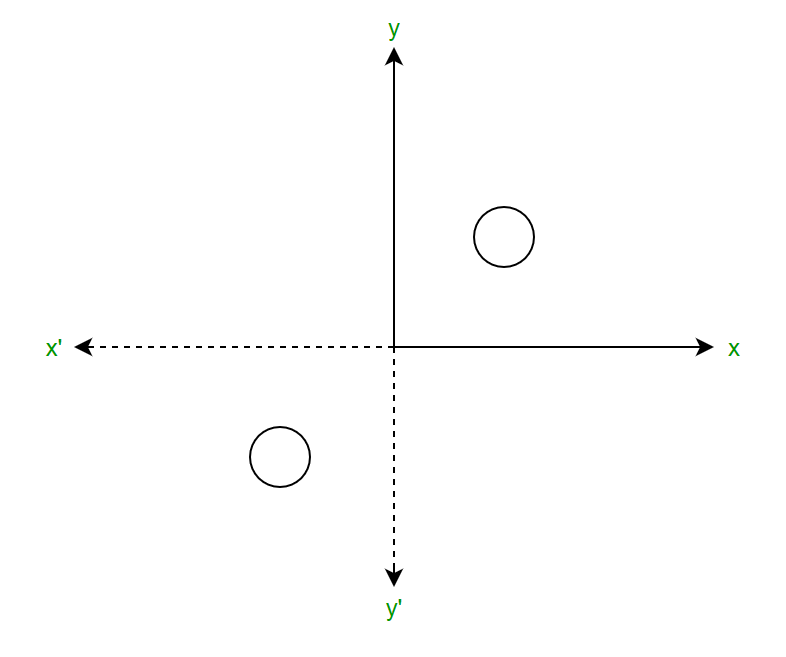
A point reflection is just a type of reflection In standard reflections, we reflect over a line, like the yaxis or the xaxisFor a point reflection, we actually reflect over a specific point, usually that point is the origin $ \text{Formula} \\ r_{(origin)} \\ (a,b) \rightarrow ( \red a , \red b) $A reflection (or flip) is one kind of transformation The reflection of a point is another point on the other side of a line of symmetry Both the point and its reflection are the same distance from the line The following diagram show the coordinate rules for reflection over the xaxis, yaxis, the line y = x and the line y = x Scroll down– Properties of Reflections Graph and Describe the Reflection (Examples #14)
Reflections across y=x Click and drag the blue dot and watch it's reflection across the line y=x (the green dot) Pay attention to the coordinatesThe Reflection X Client Wizard steps you through the configuration process—gathering information on the target host system, security settings, and client command line It even generates a startup shortcut for future use Reflection X also offers quickstart templates for configuring your X server https//wwwyoutubecom/watch?v=KMPrzZ4NTtc 18 Higher Mathematics Solved Paper https//wwwyoutubecom/watch?v=DtGuf2EJ3NY&list=PLJma5dJyAqrnj6d12DVfvBqO
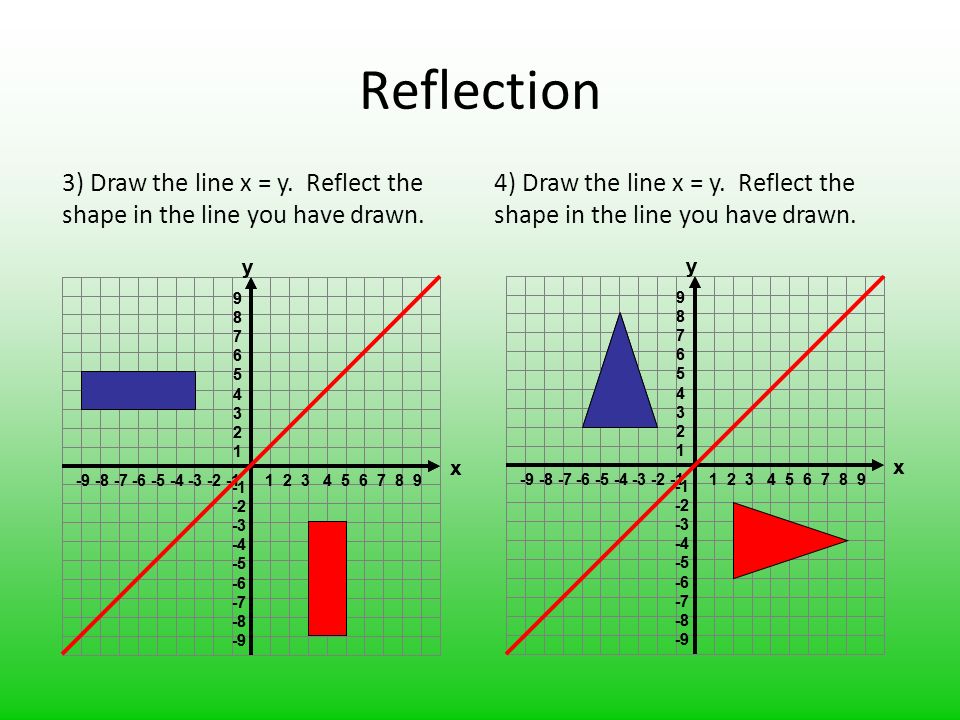
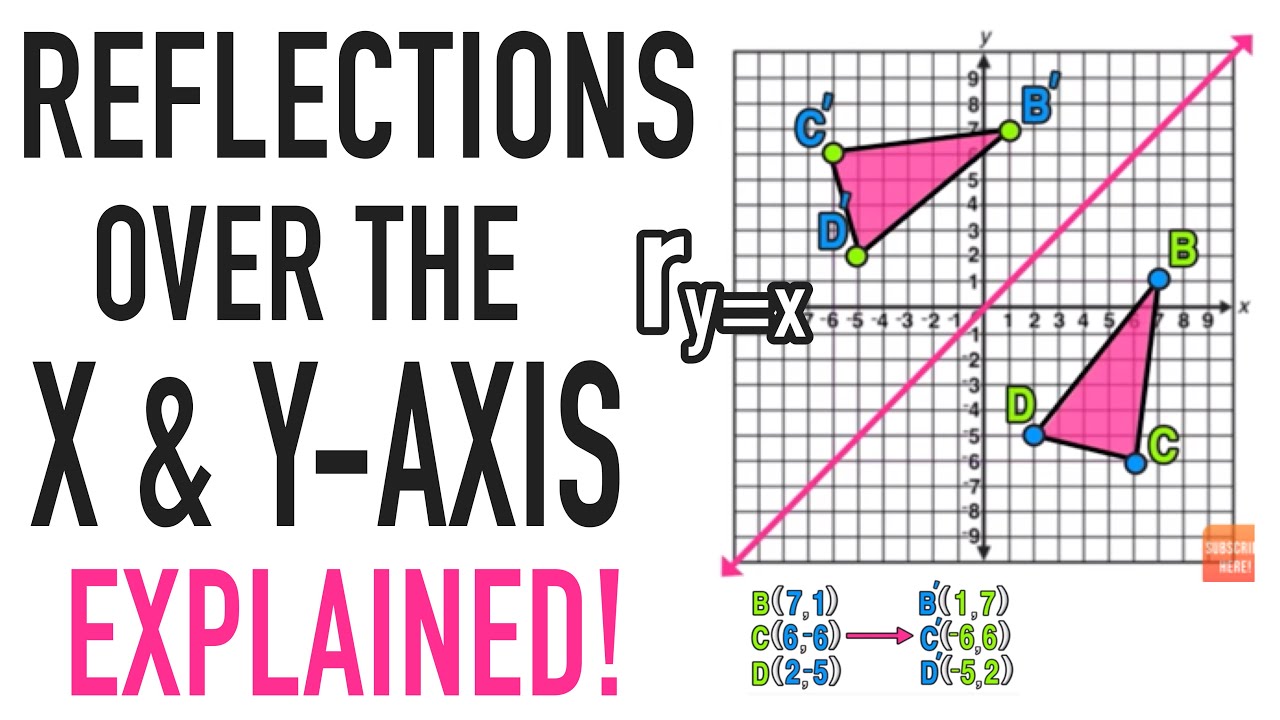
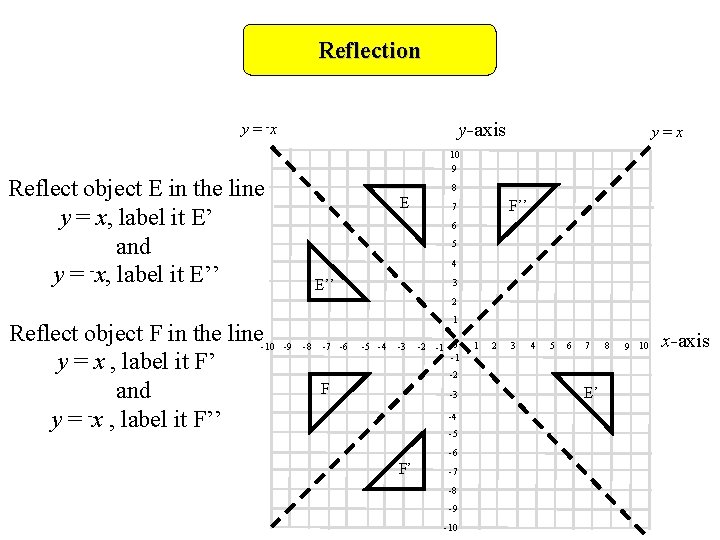
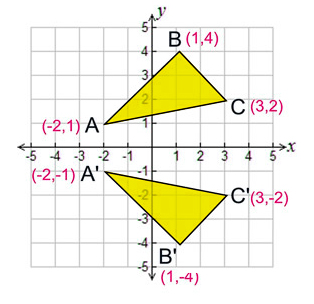
Reflections across the line y = x A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC has vertices A (This is a KS3 lesson on reflecting a shape in the line y = −x using Cartesian coordinates It is for students from Year 7 who are preparing for GCSE This page includes a lesson covering 'how to reflect a shape in the line y = −x using Cartesian coordinates' as well as a 15question worksheet, which is printable, editable and sendable How do you prove that the point P (x,y) becomes P' (y,x) after reflecting upon the line y=x?



Half A Dozen Ways To Halfturn Times Line Reflection



Www Pmschools Org Site Handlers Filedownload Ashx Moduleinstanceid 701 Dataid 3615 Filename 15 transformations answers Pdf
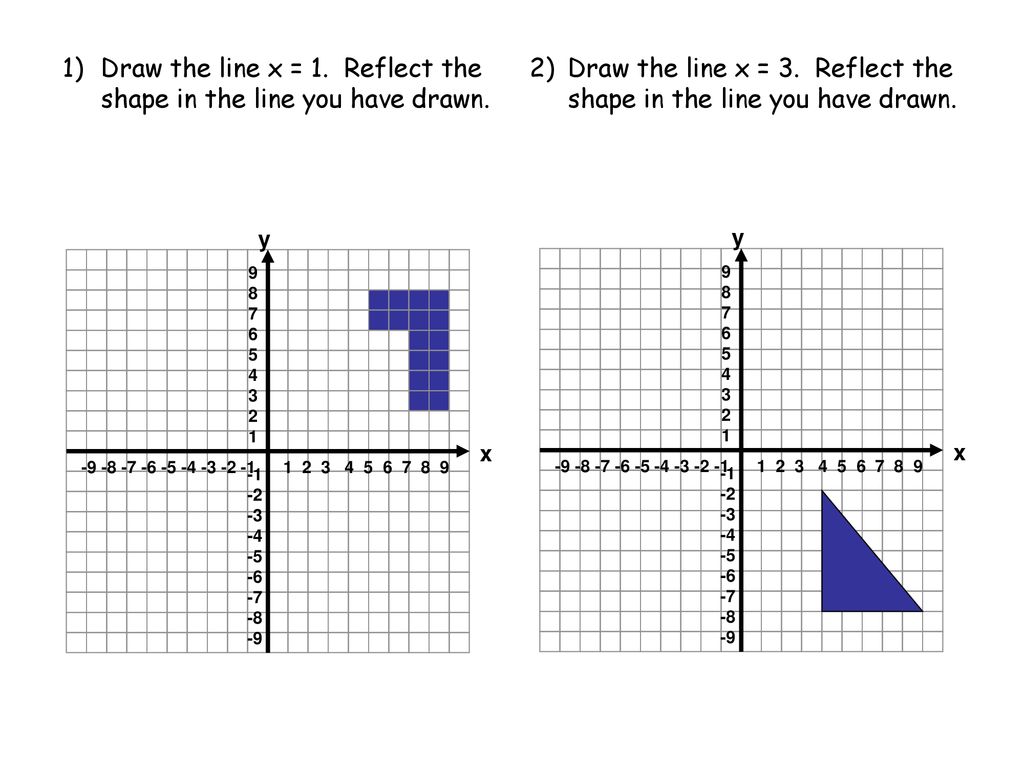
Reflections in Math Applet Interactive Reflections in Math Explorer Demonstration of how to reflect a point, line or triangle over the xaxis, yaxis, or any line x axis y axis y = x y = x Equation Point Segment Triangle Rectangle y = If f (x) Makes you reflect over the x axis Then e^x will do a neccesary reflection for reflecting it about y = 2 Then I add 2 to the end of f (x) = (e^x)2 = 2e^x Although on my homework they say the correct answer is 4 e^x Saying I needed to time 2 for some reason, which is where I lose understandingAnd also, the line x = 2 (line of reflection) is the perpendicular bisector of the segment joining any point to its image Students can keep this idea in mind when they are working with lines of reflections which are neither the xaxis nor the yaxis




Transformations Of Graphs




What Is The Image Of 6 4 After A Reflection Over The Line Y X Homeworklib
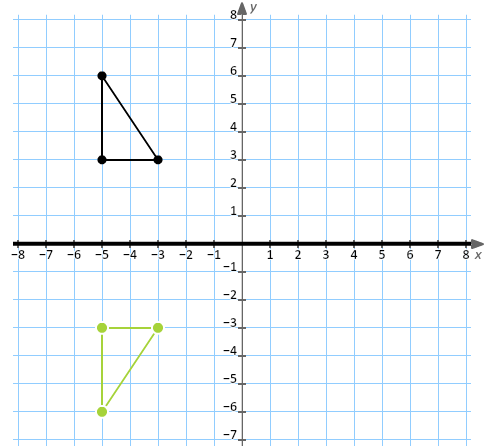
Reflection in a Line A reflection over a line k (notation r k) is a transformation in which each point of the original figure (preimage) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line Remember that a reflection is a flip Under a reflection, the figure does not change sizeExtend the line from the vertices to the opposite side of the mirror line by the same distance Mark the position of the new vertices Draw lines to join the new vertices Label the points of the reflected image as A', B', C', A reflection in a line produces a mirror image in which corresponding points on the original shape are always the 4 Reflection along with the line In this kind of Reflection, the value of X is equal to the value of Y We can represent the Reflection along yaxis by following equation Y=X, then the points are (Y, X) Y= – X, then the points are ( – Y, – X) We can also represent Reflection in the form of matrix – Homogeneous Coordinate




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3



Transformations Objective To Develop An Understanding Of The Four Transformations Starter If 24 X 72 16 Find The Value Of 1 2 8 X 72 2 Ppt Download
∴ Image of the point P (x, y) under the reflection about the line y = x is the point P (y, x) Hence, if R denotes the reflection in the line y = x, then R P (x, y)→ P' (y, x) Reflection in the line y = x y = x is an equation of the line which makes an angle of 135° with the positive direction of X axisSelina Concise Mathematics Part II Solutions for Class 10 Mathematics ICSE, 12 Reflection (In xaxis, yaxis, x=a, y=a and the origin ;The reflection of the point (4, 13) in the line 5x y 6 = 0 is



Reflection Objectives D Grade Reflect Shapes In Lines



1
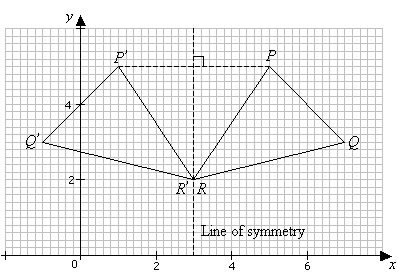
The Reflection of the Point (4, −13) About the Line 5x Y 6 = 0 is CBSE CBSE (Commerce) Class 11 Textbook Solutions 79 Important Solutions 14 Question Bank Solutions 6793 Concept Notes & Videos 3 Syllabus Advertisement Remove all ads The Reflection of the Point (4, −13) About the Line 5x Y 6 = 0 is MathematicsThere are at least two ways of doing so Method 1 The line y = 3 is parallel to xaxis Let the required image is P′ By common sense, we know (Distance between the line y = 3 and point P) = (Distance between line y= 3 and point P′) Since line joinM is (3/2, 27/2) The reflection point is (3–4, 2713) =



Reflection Of A Point In X Axis Reflection Of A Point Reflection



What Does It Mean To Reflect Over The Y X Line Quora
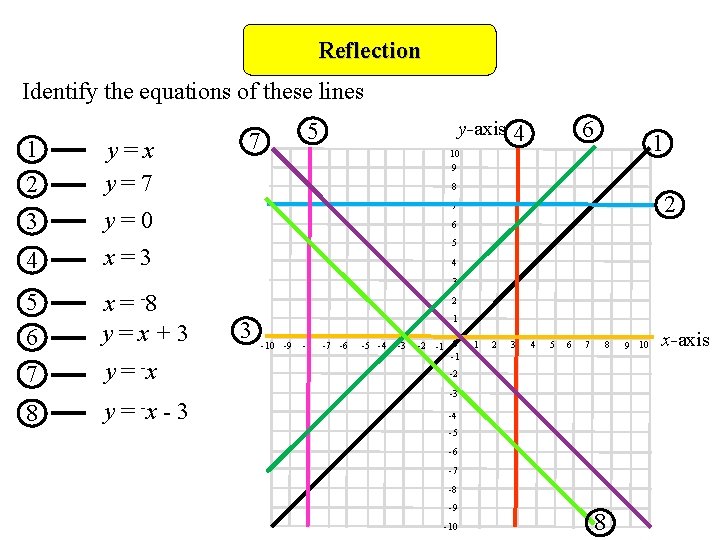
The equation of the __ line through P(4, 13) is x 5y = 4 65 = 69 The intersection of the 2 lines is the mid point M of the 2 lines 26x = 69 30 = 39;In a reflection transformation, all the points of an object are reflected or flipped on a line called the axis of reflection or line of reflection Example A reflection is defined by the axis of symmetry or mirror lineIn the above diagram, the mirror line is x = 3Solution Below is a picture of part of the plane showing the point and its reflection over the line The small boxes in the grid are each by Note that the axes in this picture are not the normal axes the usual axis is the set of points where and the usual axis is the set of points where Here instead of the axis we look at the set



Www Cabarrus K12 Nc Us Cms Lib Nc Centricity Domain 4633 U1 review answers Pdf




Reflection Over The X And Y Axis The Complete Guide Mashup Math
Advanced Math questions and answers (b) The transformation k is the reflection in the line y = x 7 By using the translation h that maps the point (0,7) to the origin, and its inverse h1, find the affine transformation k in the form k (x) Bxb, where B is a 2 x 2 matrix and b is a column vector with two components 5Video Lecture on Reflection of a Point About Line Y=x in Transformation of Chapter 2D Transformation of Subject Computer Aided Design for Mechanical EngineerFor example, when reflecting the point (2,5) over y=x it becomes (5,2) This is very simple, but why does it work?



Computer Graphics Reflection Javatpoint



Reflect The Shapes In The Mirror Lines Ppt Download
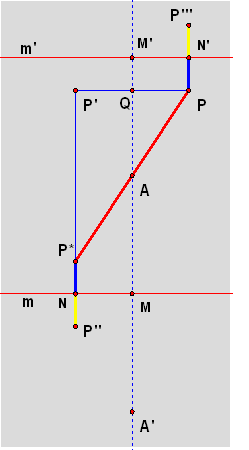
Reflecting shapes diagonal line of reflection Reflecting shapes Practice Reflect shapes This is the currently selected item Next lesson Dilations Reflecting shapes Our mission is to provide a free, worldclass education to anyone, anywhere Khan Academy is a 501(c)(3) nonprofit organization Donate or volunteer today!We are now going to reflect the point (–3, 5) in the line 3x – y – 6 = 0 and find the point of reflection The plan is as follows First find a vector that is perpendicular to the line 3x – y – 6 = 0 going from the point (–3, 5) to the point P = (x, y), which lies on the line This will be the normal vector t (see the diagram)Related Pages Properties Of Reflection Transformation More Lessons On Geometry What is Reflection?



Mathscene Vectors Lesson 5




Solved 6 Reflection Matrices And Connection To Rotations Chegg Com
Invariant Points) Mathematics explained in detail by experts to help students prepare for their ICSE exams $\begingroup$ The first basis vector should stay fixed (since it lies on the line) and the other should be reflected Correct?Flip over a line;




What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic



Reflections Over The X Axis And Y Axis Explained Youtube
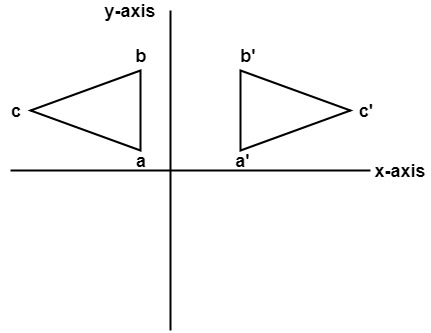
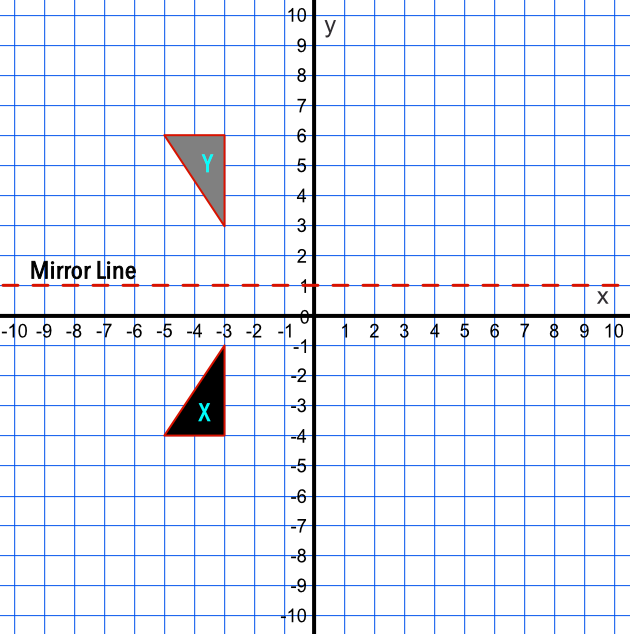
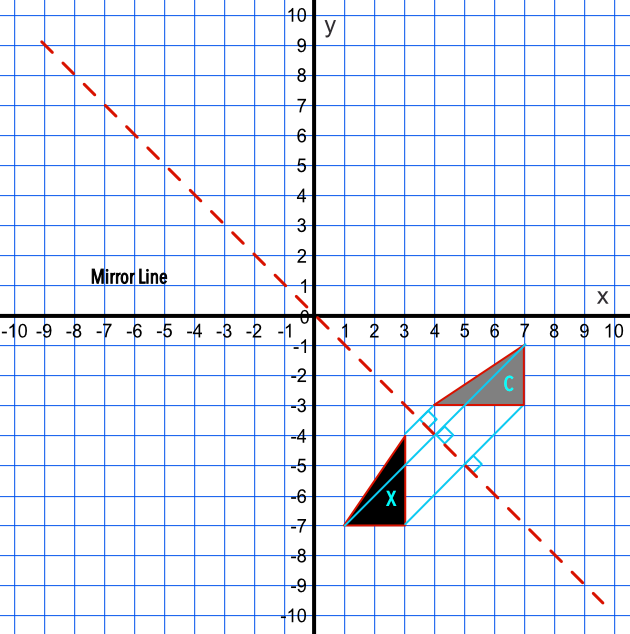
X y 6) reflection across y = −2 H(−1, −5), M(−1, −4), B(1, −2), C(3, −3) x1©t 32u0 c1Z2 9 UK Ru3t zaw jS IoZfbtzw YaArOev bLILECM1 C yAel 5l Q hrUiPgzhVtWsq Hrje nsSetrKvCe wd2V z rM jard0e K Hwai dt OhZ ZI8nfDiFnTiJt BeZ SPKrMeg 4AklDgfeXblr gai gReflections A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a fixed line The fixed line is called the line of reflectionA reflection in a line produces a mirror image in which corresponding points on the original shape are always the same distance from the mirror line The reflected image has the same size as the original figure, but with a reverse orientation




Reflection Objectives D Grade Reflect Shapes In Lines




What Is The Equation For The Line Of Reflection X 6 Y 6 Y X Y 2 Brainly Com
Reflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3)Invariant Points) All the solutions of Reflection (In xaxis, yaxis, x=a, y=a and the origin ;Line segments I end this segment i n over here and T oh this is T oh here are reflected over the line y is equal to negative X minus 2 so this is the line that they're reflected about this dashed purple line and it is indeed y equals negative X minus 2 this right over here is in slopeintercept form the slope should be negative 1 and we see that the slope of this purple line is indeed negative




Reflection Transformation Solutions Examples Videos




Reflection Transformation Matrix
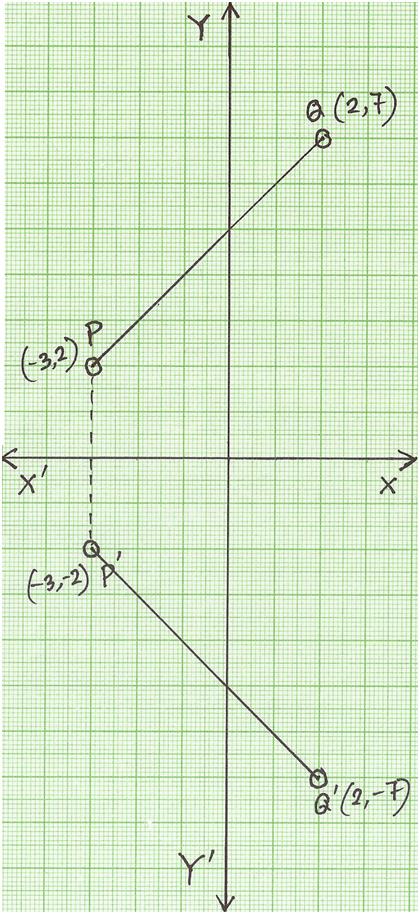
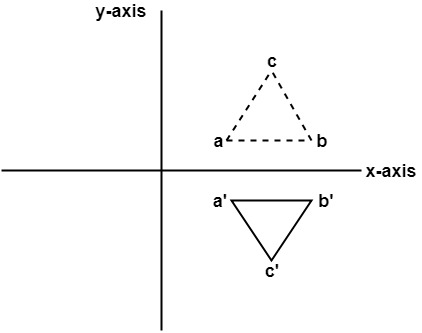
Reflection line points Share Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeThe reflection of the point (x, y) across the line y = – x is (y, x) Reflection in a Point A reflection point occurs when a figure is constructed around a single point known as the point of reflection or centre of the figure For every point in the figure, another point is found directly opposite to it on the other side Under the point




How To Find Coordinates Of Reflected Point Mathematics Stack Exchange



Reflection Over The X And Y Axis The Complete Guide Mashup Math
Thus, P' is the reflection of P in the line x = 4 Hence, the coordinates of P' are (6, 3) ML Aggarwal Solutions for Class 10 Maths Chapter 10 Reflection (ii) The steps are (a) Draw axis XOX' and YOY' and take 1 cm = 1 unit (b) Plot point P (2, 3) on itBackground Tutorials Use a pair of perpendicular number lines, called axes, to define a coordinate system, with the intersection of the lines (the origin) arranged to coincide with the 0 on each line and a given point in the plane located by using an ordered pair of numbers, called its coordinatesX = 3/2 y = 6 15/2 = 27/2;



Ks2 Year 6 Reflections Of Shapes In X Y Y X And Y X For Challenge Word And Pdf Great Practice Teaching Resources



Www Westada Org Cms Lib8 Id Centricity Domain 2401 Reflection hw key Pdf
In order to reflect about the line y=5, we first need to reflect about the line y=0 (which is much easier) To do that, simply shift the graph 5 units down (to effectively move the line to ) Algebraically, you just subtract 5 from to get Now to reflect over the line (the xaxis), simply replace "y" with "y" to get11 Solve xy6 = 0 Tiger recognizes that we have here an equation of a straight line Such an equation is usually written y=mxb ("y=mxc" in the UK) "y=mxb" is the formula of a straight line drawn on Cartesian coordinate system in which "y" is the vertical axis and "x" the horizontal axis InGet the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha



Reflection Objectives D Grade Reflect Shapes In Lines



Computer Graphics Reflection Javatpoint
The reflection of the point (4, 13) about the line 5x y 6 = 0 is A (1, 14) B (3, 4) C (0, 0) D (1, 2) Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesTherefore, X, Y is the reflection of point and is changed as X, Y in the region of YAxis A Condition of Reflection when Y = X Take the case where a point is reflecting across a line Y=X Now, the X and Y coordinates will interchange their positions However, the signs get negated/cancelled when the point of reflection takes place over For example, when point P with coordinates (5,4) is reflecting across the Y axis and mapped onto point P', the coordinates of P' are (5,4)Notice that the ycoordinate for both points did not change, but the value of the xcoordinate changed from 5 to 5 You can think of reflections as a flip over a designated line of reflection
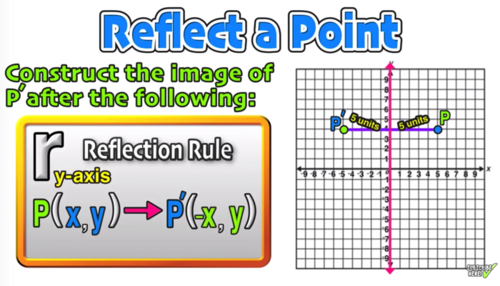



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Transformations Bluesmartie15
Describe the reflection by finding the line of reflection Determine the number of lines of symmetry Find a point on the line of reflection that creates a minimum distance Video – Lesson & Examples 58 min Introduction to Reflections;Click here👆to get an answer to your question ️ The reflection of the point (4, 13) in the line 5x y 6 = 0 Join / Login maths The reflection of the point (4, − 1 3) in the line 5 x y 6 = 0
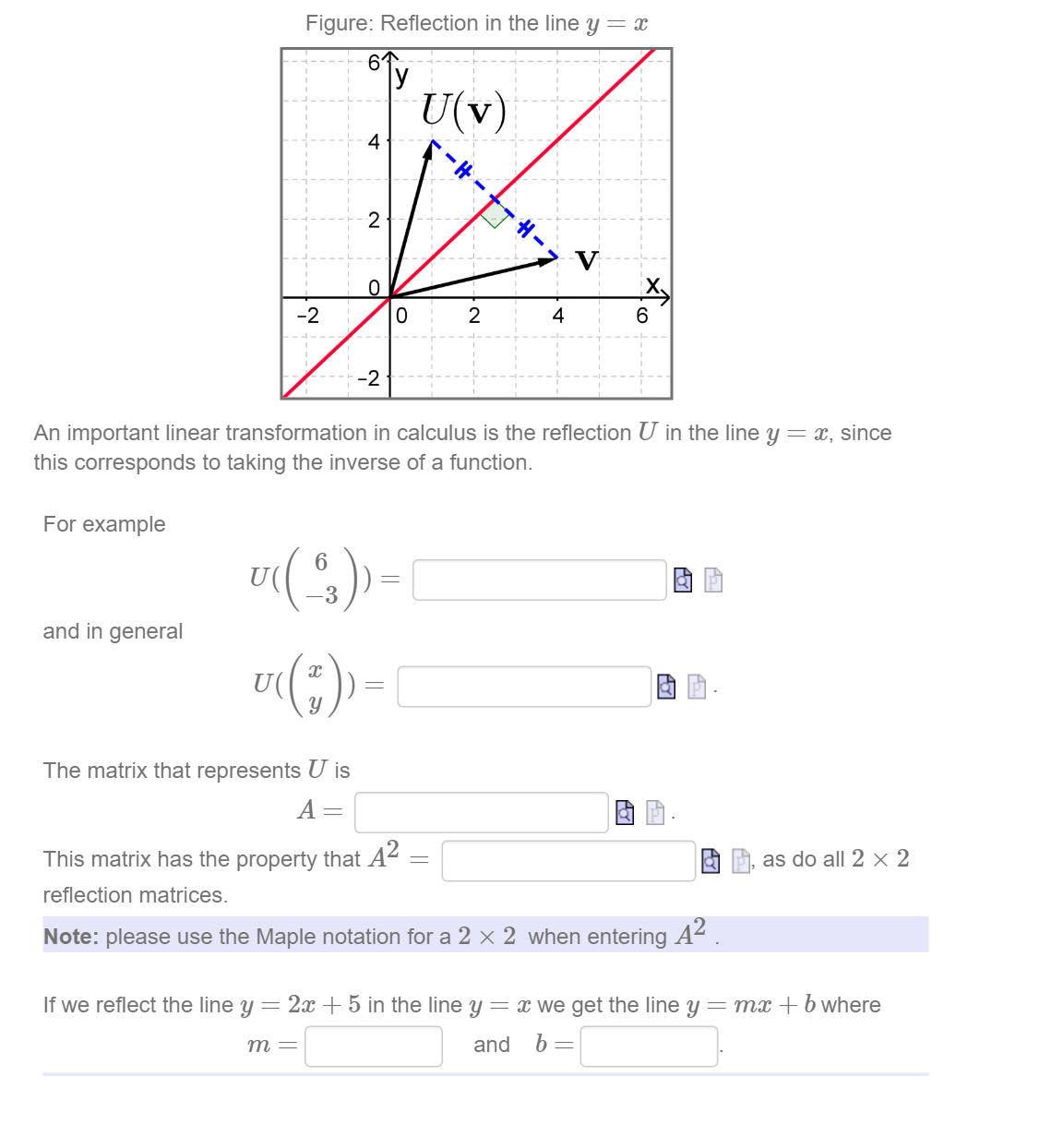



An Important Linear Transformation In Calculus Is The Chegg Com




Geometry Transformations




Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Translations Rotations And Reflections Ck 12 Foundation



Http Www Lcps Org Cms Lib4 Va Centricity Domain Transformations packet key Pdf




An Illustration Of The Design Criteria And The Cp Reflection Of The Download Scientific Diagram



Matrices As Transformations
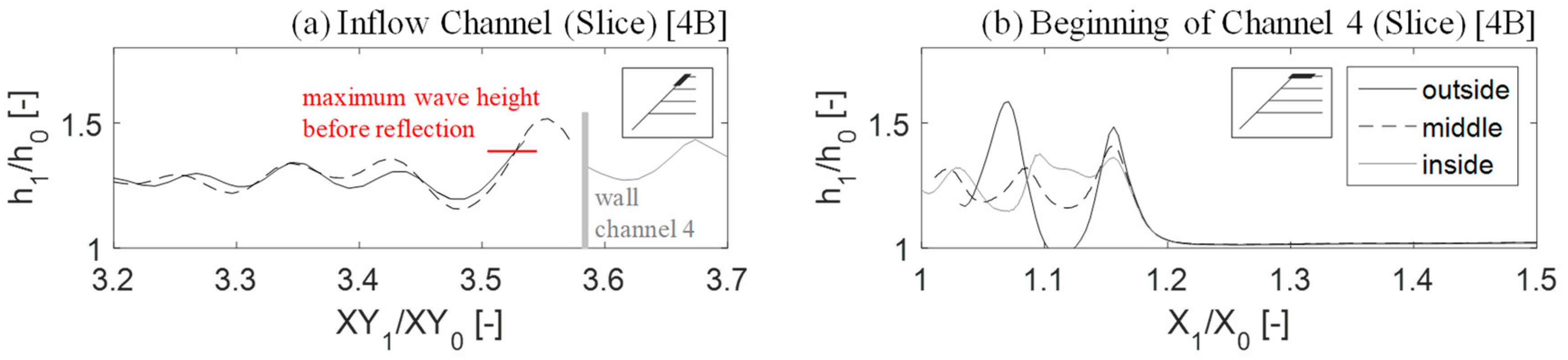



Water Free Full Text Reflection Phenomena In Underground Pumped Storage Reservoirs Html



What Is The Image Of 2 5 Reflected Across X 2 Socratic



Reflection In 2d Graphics Geeksforgeeks



Reflection Transformation Solutions Examples Videos



Sequence Transformations Glide Reflections Mathbitsnotebook Jr




Reflect The Shapes In The Mirror Lines Ppt Download



Www Pmschools Org Site Handlers Filedownload Ashx Moduleinstanceid 701 Dataid 3614 Filename 15 composition of transformations answers Pdf




Reflecting Shapes Article Reflections Khan Academy




Learn About Reflection Over The Line Y X Caddell Prep Online




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3




Reflection




Let C 1 Be The Graph Of Xy 1 And The Reflection Of C 1 In




Reflection Mathbitsnotebook A1 Ccss Math



Www Cgsd Org Site Handlers Filedownload Ashx Moduleinstanceid 215 Dataid 1165 Filename 255 Smp Seaa C04l06 Pdf




Reflection In The Line Y X Transformation Matrix Youtube




Transformation Reflection Over The Line Y X Youtube



Point Reflection Wikipedia



Reflection In A Cartesian Plane Lexique De Mathematique




Normalized Values Of The Element Of Reflection Matrix R Xy R Yx Download Scientific Diagram



The Point P 3 4 Is Reflected To P In The X Axis And O Is The Image Of The Origin O When Reflected In The Line Pp What Are The Coordinates Of O
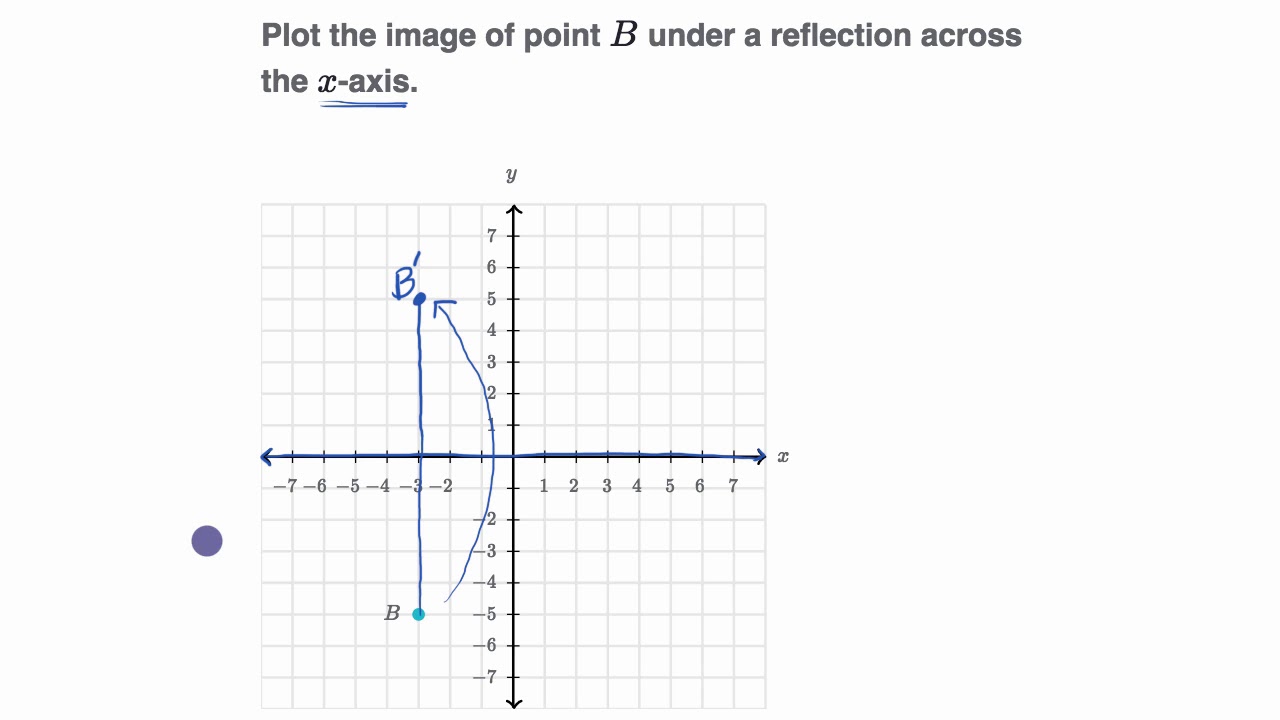



Reflecting Points Video Reflections Khan Academy




Reflection Definition Reflection In The Coordinate Plane
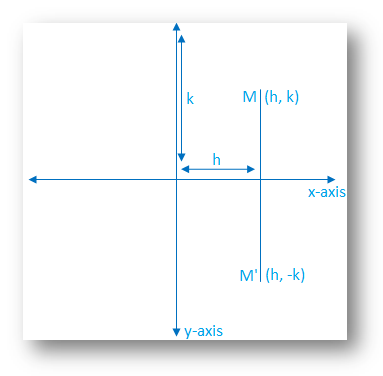



Reflection Of A Point In X Axis Reflection Of A Point Reflection
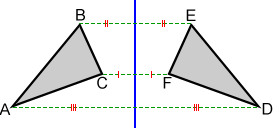



Reflection
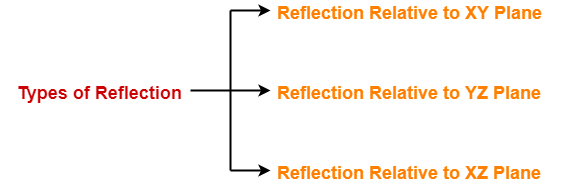



3d Reflection In Computer Graphics Definition Examples Gate Vidyalay




A Line Segment Goes From 1 2 To 4 1 The Line Segment Is Reflected Across X 1 Reflected Across Y 3 And Then Dilated About 2 2 By A Factor
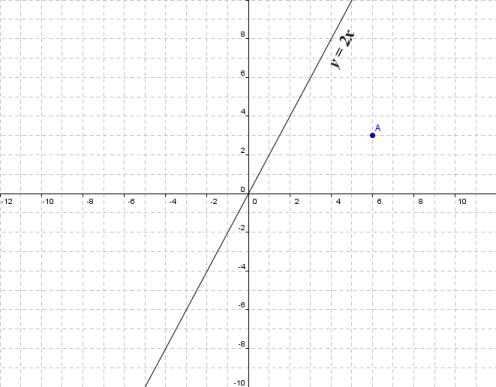



Matrices As Transformations
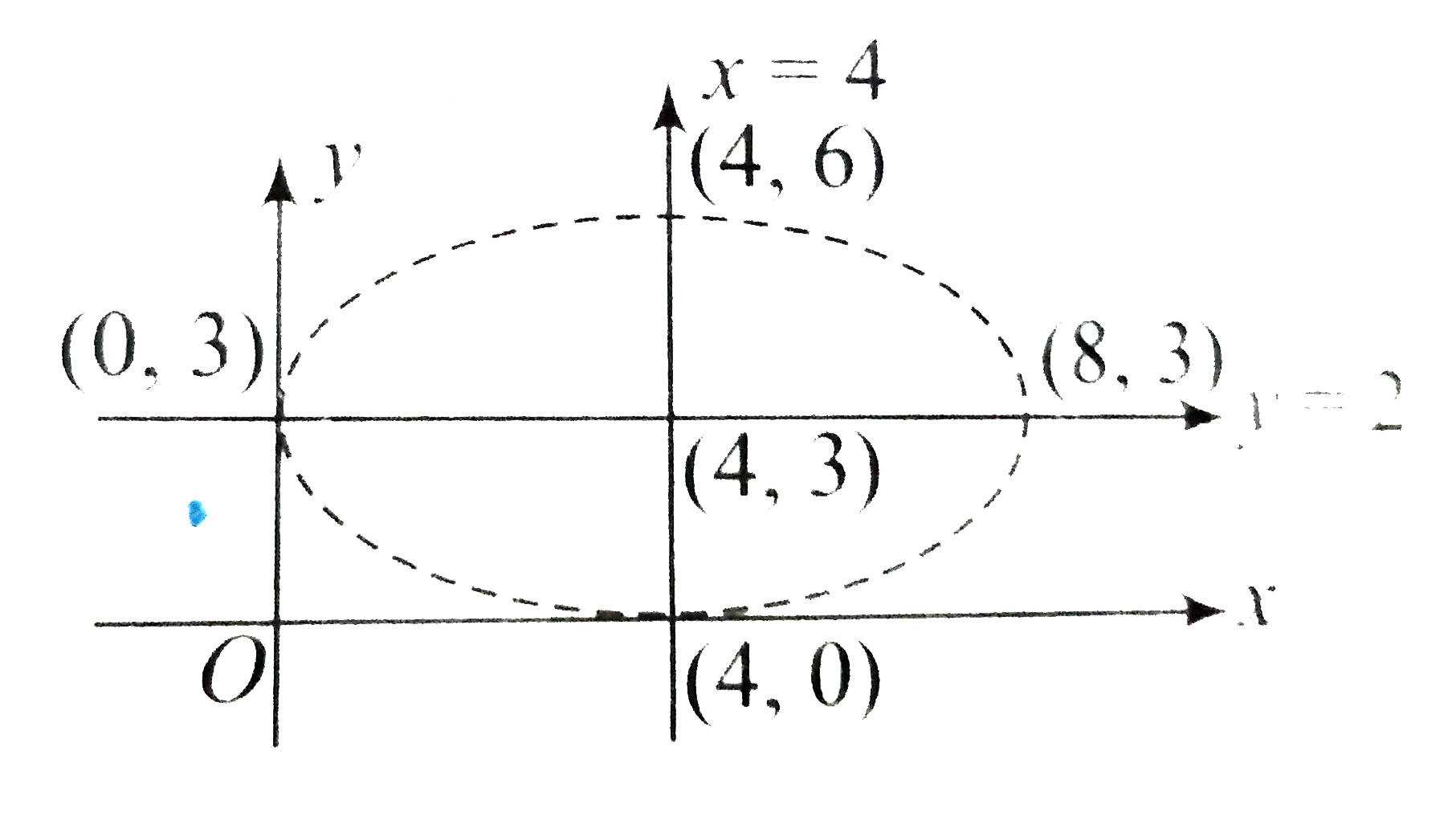



If The Reflection Of The Ellipse X 4 2 16 Y 3 2 9
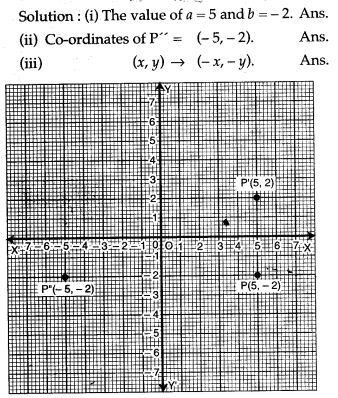



Icse Solutions For Class 10 Mathematics Reflection A Plus Topper




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Reflection Notes Videos Qa And Tests Grade 9 Optional Mathematics Transformation Kullabs




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Reflection




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



How To Reflect A Graph Through The Y Axis Studypug



What Does It Mean To Reflect Over The Y X Line Quora



Reflection




Bab11 Mathf2




Chapter 12 Reflection In X Axis Y Axis X A Y A And The Origin Invariant Points Selina Concise Mathematics Part Ii Solutions For Class 10 Mathematics Icse Topperlearning



Reflection Definition Reflection In The Coordinate Plane




Q 15 Options Two Lines Frac X 3 1 Frac




Reflecting Shapes Article Reflections Khan Academy




Rules For Reflections Read Geometry Ck 12 Foundation




Reflections Through The Axes And The Lines Y X And Y X Geogebra



Combination Of Transformations Notes Videos Qa And Tests Grade 10 Optional Mathematics Transformation Kullabs



Www Sd308 Org Cms Lib Il Centricity Domain 1447 Geometry chapter 9 Chapter 9 review key Pdf



Reflection



1




What Is The Equation For The Line Of Reflection X 6 Y 6 Y X Y 2 Brainly Com




Reflection Transformation Matrix




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
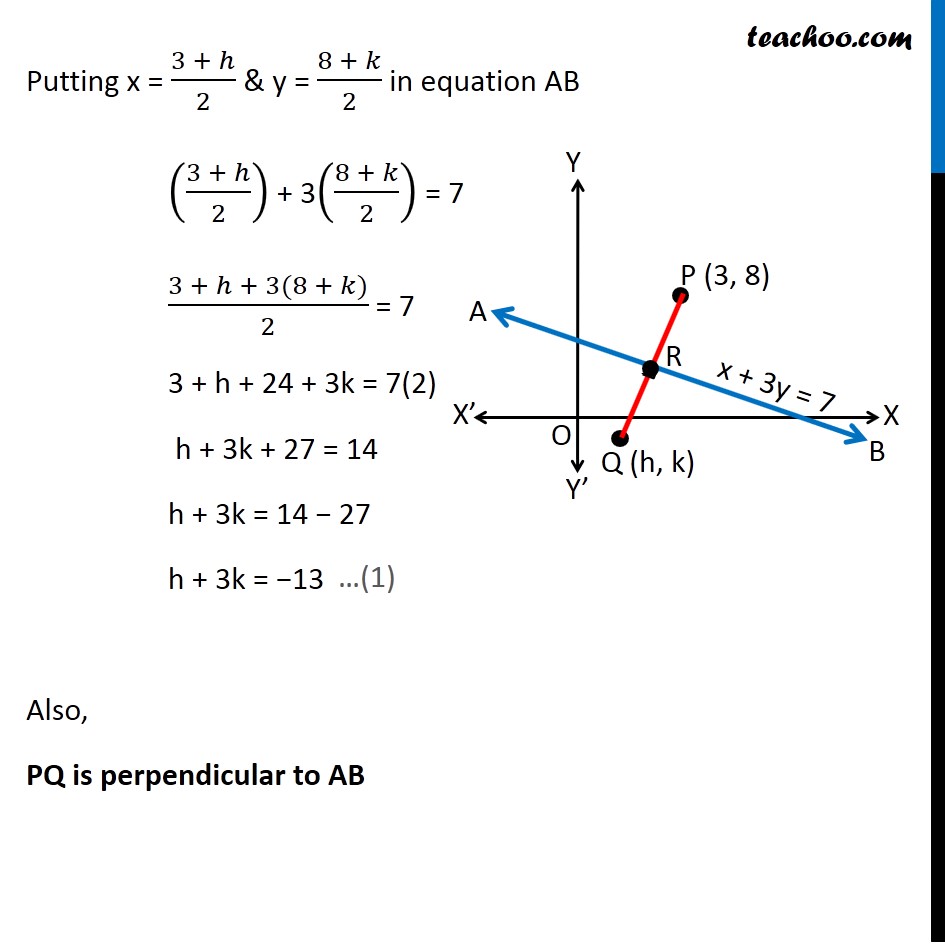



Misc 18 Find Image Of 3 8 With Respect To Line X 3y 7



Reflection Brilliant Math Science Wiki
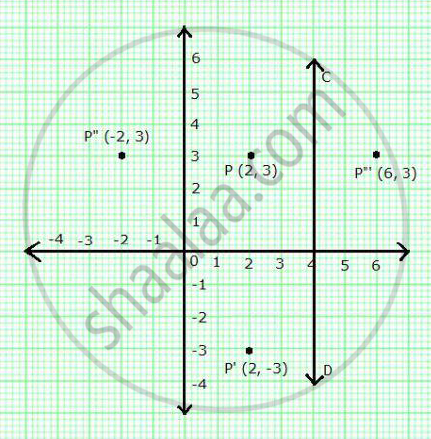



A Point P A B Is Reflected In The X Axis To P 2 3 Write Down The Values Of A And B P Is The Image Of P Reflected In The Y Axis




Selina Concise Mathematics Class 10 Icse Solutions Reflection A Plus Topper




Geometry Reflection




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3




Coordinate Geometry Reflections On A Coordinate Plane Magoosh Math



1



Schoolwires Henry K12 Ga Us Cms Lib08 Ga Centricity Domain 26 7th and 8th grade math 8th grade flexbook Unit 1 sections 1 23 1 4 rules for reflections Pdf



1
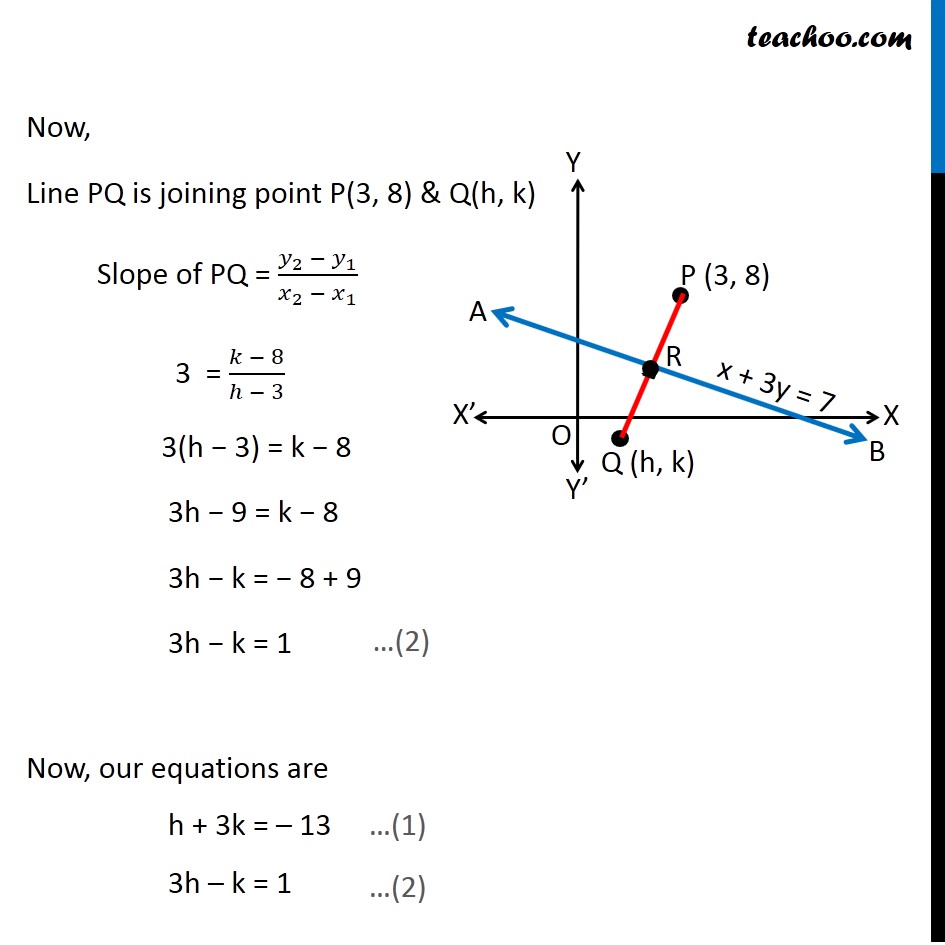



Misc 18 Find Image Of 3 8 With Respect To Line X 3y 7



Reflect Triangle Over X Axis Y Axis Y X Y X Geogebra




Geometry Transformations



Mathscene Vectors Lesson 5




Reflections


