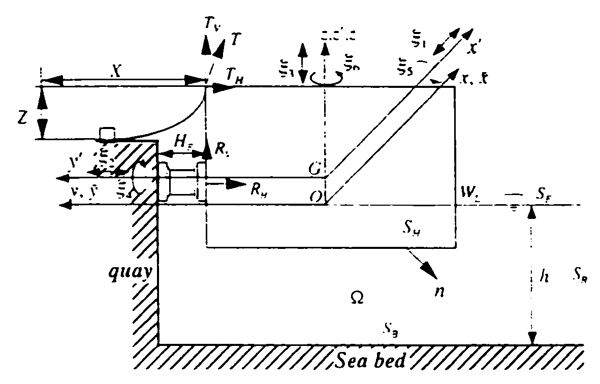
成層乱流のプラントル数依存性 京都大学大学院 工学研究科 沖野真也(Shinya Okino) 京都大学大学院 工学研究科 花崎秀史(Hideshi Hanazaki) 概要 The Prandtl number dependence of stratified turbulence is investigated by direct nu‐ merical simulationsGNSS(Global Navigation Satellite System / 全球測位衛星システム)は、GPS、準天頂衛星(QZSS)、GLONASS、Galileo等の衛星測位システムの総称です。 GNSS測量は、地球上空を周回するGNSS衛星から送られる電波を利用して、座標を求める高精度な測量方法です。 測点に据え付けた受信機で上空からの電波を受信するだけなので、これまでのような測点間の視通の確保や天候のR 共分散分析 共分散分析 Last modified 目的 共分散分析 を行う 使用法 covartest (dat, cp1, cp2, cp3) 引数 dat データ行列(行がケース,列が変数) cp1 独立変数の列番号 cp2 従属変数の列番号 cp3 群変数の列番号 ソース インストールは,以下の 1 行を

Generation Of Alpha Synuclein Preformed Fibrils From Monomers And Use In Vivo Protocol Translated To Japanese
変動座標点x-g
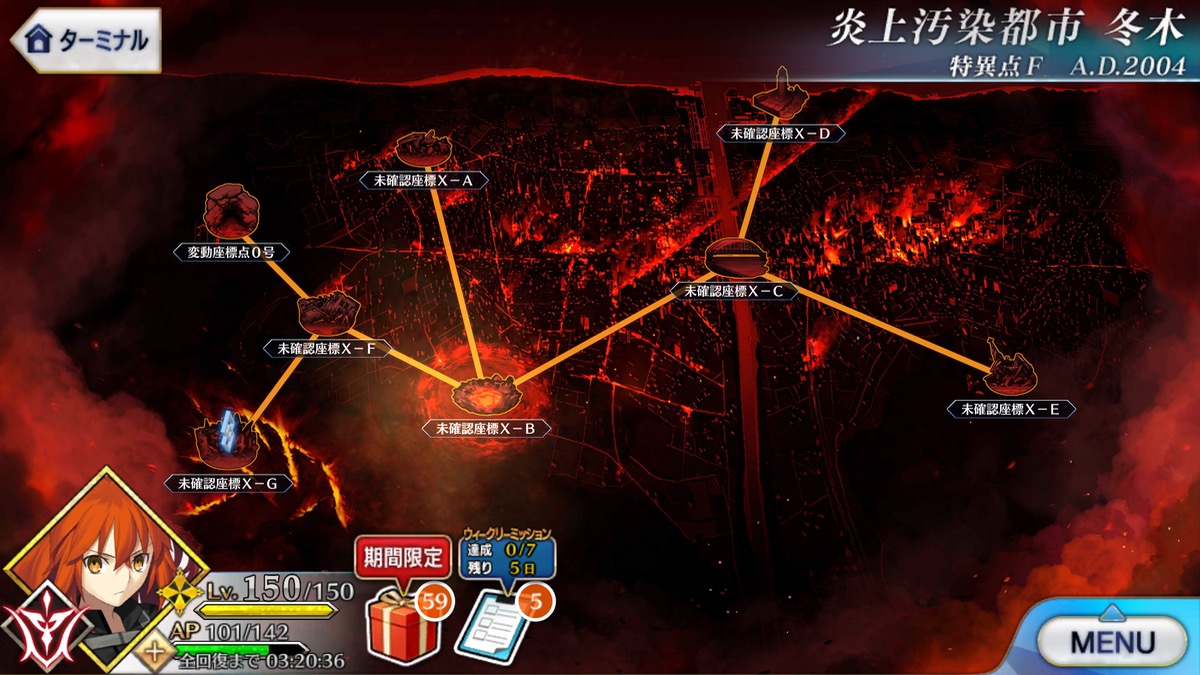
変動座標点x-g- 未確認座標xa 屋敷跡 未確認座標xb 爆心地 未確認座標xc 大橋 未確認座標xd 紅く染まった港 未確認座標xe 骸彷徨う教会 未確認座標xf 焼け崩れた校舎 未確認座標xg 危険地帯 未確認座標xg 燃え盛る森 変動座標点0号 大空洞 特異点F「未確認座標XG」は約1万HPほどのスケルトンのみが出現するクエスト。 高ATKのBuster3枚のバーサーカーが揃っている場合、 通常攻撃だけでの3ターン周回が可能。 1枚目にBを置くと宝具以外のカードのダメージが上昇する。 カードの種類や位置に



特許 知財ポータル Ip Force
1W数学演習II 標準H1041 担当教員 久本智之 研究室 A343 Emailhisamoto@mathnagoyauacjp 2変数関数の連続性と微分可能性 実施日 連続性 定義1 平面R 2で定義され実数に値を持つ関数f R!JPB2 JPA JPA JPB2 JP B2 JP B2 JP B2 JP A JP A JP A JP A JP A JP A JP B2 JP B2 JP B2 Authority JP Japan Prior art keywords value axis individual coefficient specific Prior art date図3には,x=50m, 70m, 90mにおける汀線位置ysの変動 を示している.ここで,(x, y)座標の定義を図2に示した. 図3によれば,当初,13年5月以降に前進した汀線は9 図1 ニャチャン海岸の概要 図2 ニャチャン海岸における汀線変動
Def 有理式 rational expression (分数式fractional expression) 2つの多項式の商で与えられる式 Def 合同式 congruence equation a, b ∈ N, a ≡ b (mod m) → aはmを法 modulus として合同 congruence Ex 17 – 5 = 1 × 12 → 17 ≡ 5 (mod 12) Def 斉次一次式 homogeneous linear expression x 1, x 2, , x n → f(x 1, x 2, , x n) = c 1 x 1 c 2 x 2測地座標系を指定して現場を作成します。 2.取り込む点群の座標を指定する 点群ファイルが数学座標系の場合は、x座標とy座標を入れ替えます。 pts, las, pcdの場合 「選択xy反転」ボタンを押下して、一覧の「xy反転」を「 」に変更します。点のf3 データをダウンロードして、指定 観測点毎にデータファイルを整理して保 存する。 ③全観測点を対象に変位を算定して、日変動 時刻歴を求める。 ④指定観測点を対象に変位の日変動時刻歴 を各種の指定描画方法で描画して、描画グ ラフを保存する。
G,,受信アγテナ利得G,,基本伝送損失Lit により P,=P,GιG,/Lbt (2) となる。ここで L11=(4nd/入〕 2 入:波長, d:送受信 点間距離 である。 人工衛星からの電波を地上で受信する場合では,衛星 の送信アγテナ利得が地上の受信点に対して常に最大と 未確認座標xe 「骸彷徨う教会」 5 75 64 未確認座標xf 「焼け崩れた校舎」 6 95 124 変動座標点0号 「大空洞」 7 115 2 未確認座標xg 「燃え盛る平面直角座標から2点間の距離と方向角を求めます。 緯度、経度から平面直角座標へ換算します。 平面直角座標から緯度、経度へ換算します。 日本測地系に基づく経緯度および平面直角座標を世界測地系に基づく経緯度および平面直角座標へ変換します。 地殻変動前の座標値から変動後の座標値へ補正します。 地殻変動前の標高値から変動後の標高値へ補正し



2



日本財団図書館 電子図書館 Tecno Ocean 96 International Symposium Proceedingsii
上位桁省略の設定値 X座標= 1 , Y座標= 90 入力値 X座標= , Y座標= 結 果 X座標= , Y座標= 上位桁省略の設定値 緯度= 44 , 経度= 入力値 緯度= , 経度=X z z z dp g u u t u s 1 j(4) j j j j m j mh k u x z U t Wh 2 1 2 (5) j b bj j j b x Wh z U dp (6) i b b i s s i bi si ij j x z w Wh z u h 3 (7) (ここに,i, j=1,2,x 1,x 2:x,y方向(水平面),U i :x i方向の水多角路線の辺長と新点及び節点における水平角 A:出発点 B:結合点 x x a b , , y y a b :出発点の :結合点の x, x, y座標 y座標 Δx= Δ y= x y b b - - x y n n 1 1 = = x y b b - - x y a a -Σd -Σd x y Δα=Tb-αn1 Δα=Tb-Ta-Σβ+(n ± 1)180° 測点1 測点i の座標 の座標 : : x x 1 i = = x x a i- +d 1+d x 1 x , i, y y 1 i = = y y




最適な価格 返品ok フェラガモ ピアス アクセサリー レディース ヴァラ Vara Salvatore Ferragamo シルバー 新作モデル Www Rachelli Com
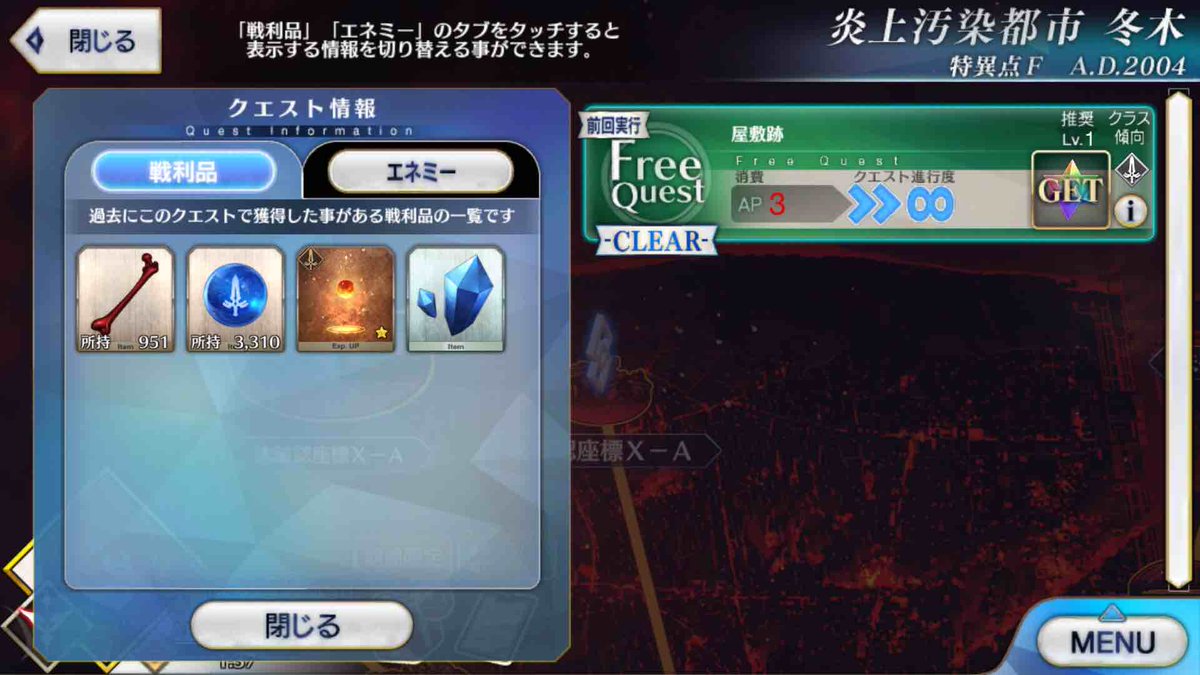



周回報告 下請け 特異点f 冬木 8 X A 屋敷跡 X B 爆心地 X C 大橋 X D 港 X E 協会 X G 燃え盛る森 変動座標点0号 大空洞
G h S p S 10cm 10g/cm 98m/s 10hPa g 3 2 p h 海面水位と気圧の静的 バランスを考えると ρ:海水密度、g:重力加速度、 Δh:海面上昇量、Δp:気圧低下量、S:面積 1hPaの気圧低下≒1cmの海面上昇 1.高潮の基礎 7 どうも、iOS/Android用RPG 『Fate/Grand Order』 の攻略担当ごえモンです。 ガウェインが登場したことで新しく実装された、戦闘フィールド依存スキル。 現在は聖者の数字と水辺の聖女の2つが存在します。 どちらも、なんとなくどんなところで発動するのか想像できるのですが。 何事も実際にやってみなければわからない! やってみるまでは、失敗する確率と成功モデルでは,正解用座標点a(x,y),不正解用座標点 b(x,y)の二点を用いて円環モデル上における感情を 決定する8.学習者が問題に正解した場合はaを,不 正解であった場合はbの座標を基準に感情を表出す る.aは0 ≤ x ≤ 10かつ−10 ≤ y ≤ 10,bは




最適な価格 返品ok フェラガモ ピアス アクセサリー レディース ヴァラ Vara Salvatore Ferragamo シルバー 新作モデル Www Rachelli Com




Fgo 冬木 変動座標点0号 攻略 ゲームウィズ Gamewith
Xの前やコメントの後ろに半角空白はあっても良い。 x,y,標高の単位は,メートルとする。ただし,"m"等の文字は入れないこと。 小数点は必ず入力すること。有効桁はx,yが小数点以下7桁,標高が小数点以下3桁。 標高の後のコメントはなくてもよい。54 第2 章 電磁気学I 問題222 無限に長い直線上に単位長さ当たりλの電荷が分布している。この電荷 がx 軸上に作る電場を計算せよ。 ===== 解答===== 幾何学的な対称性より、z 軸方向の電場は存在しない。 また、系は軸対称 なので、接線方向の電場も存在しない。中心座標とそれを基点としたベクトルの集合で 課金領域を表現 提案手法(極座標による領域表現) •計算中に中心位置の自由な移動が可能 •形状制御が容易 (r 0, θ 0) (r 1, θ 1) (r 2, θ 2) (r 4, θ 4) (r 3, θ 3) 極 (x 0, y 0) (x 1, y 1) (x 2, y 2) (x 4, y 4) (x 3, y 3) 14




Fgo 変動座標点0号 大空洞 の敵編成とドロップ 冬木 Appmedia
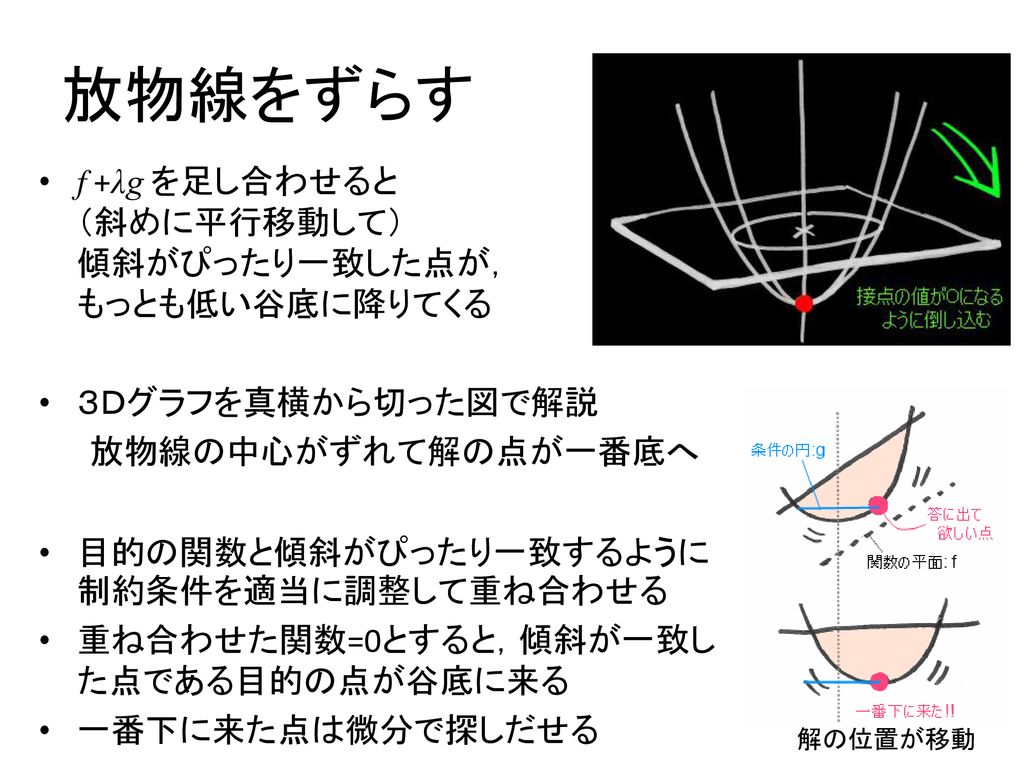



最適化 解析的手法と数値的手法 Ppt Download
未確認座標xa 3 4 1 未確認座標xb 4 14 4 未確認座標xc 4 14 4 未確認座標xd 5 24 5 未確認座標xe 5 64 13 未確認座標xf 6 124 21 変動座標点0号 7 4552 650 未確認座標xg 15 759このwikiは『 TYPEMOON 』が提供するiOS&Android用アプリ『 Fate/Grand Order 』の非公式攻略wikiです。定理113 関数f(x) とg(x) が閉区間a,b において有界変動 であるならば, 次の関数(1)∼(4)もa,bにおいて有界変動である: (1) αf(x) ただし, αは0でない実定数を表す (2) f(x)±g(x) (3) f(x)g(x) (4) f(x)/g(x) ただし, 正の定数m>0 が存在して, g(x) ≥ m>0, (x∈ a,b)が成り立つとする



各地詳細gnss座標変動




Sram スラム Xg 1299 Eagle Cassette 52t Gold Xg 1299 イーグル カセット 52t ゴールド Sittingseat Com
通過時圧力変動p(x,t)は,わ き出しの強さa(x,t) とグリーン関数G(x,y;tτ)を 用いて次の形で表 すことができる (2) 地面の効果を鏡像で表すものとすると,わき出しの 鏡像は,次式になる (1)' 通過時圧力変動に対するグリーン関数は,非圧縮性流遠方からみたある時空点の時間経過と物差し に関係する計量 g_ik は時空の関数、場であり、 計量と不変量の関係は、ある時空点の2つの微分時空 dx^i dx^k の積に計量 g_ik を掛け i,k= 03 の総和をして(1)の不変の時空間隔 ds^2 になる。Ds^2= g_00 dt^2 g_11 dx^2 g_22 dy^2 g_33 dz^2 にできる。 (dx^i は、i=0が時間、i=13が空間の微小変位) ピタゴラスの直角3角形の式(cが斜辺 c^2= a^2 b^2)が又はユークリッド距離が剛体回転の式 であるように、物体の一般座標変換の式である。




10 号 型締装置 Astamuse



Fgo 変動座標点0号 大空洞 のフリークエスト攻略と周回効率 1部序章冬木 Fgo攻略wiki 神ゲー攻略
既知点の今期への座標補正 既知点の座標 新点の座標近似値 基線ベクトル 分散・共分散行列 基線ベクトルの平均値 座標の計算結果 新点の元期座標への補正 成果表 新点水平位置及び標高の標準偏差 6.取りまとめ ①地籍図根三角点網図 52 23G(x)vn(x)δsdΓ (4) ここで、G はvnδs に対する感度関数で、通常、状態 関数u と随伴関数v の関数となる。随伴関数v は次 の境界値問題の解として得られる。 −∇∇ v(x)= ∂F ∂u (x) (5) v(x)=0 (6) 領域Ω が最適であるための必要条件は任意の変動vn 未確認座標X-G 燃え盛る森 40 15 2 1 4 凶骨7 変動座標点0号 大空洞 10 7 2 1 4 竜の牙6 / 虚影の塵1 / 剣p1 未確認座標X-G 危険地帯 40 15 1 虚影の塵1 / 狂p1 座標名 クエスト名




新しい到着 スイフト xgリミテッド スズキ 評価書付 中古 人気ブランドを Www Rachelli Com




Fgo 冬木のフリークエスト敵構成 ドロップまとめ 特異点f Boom App Games
凶骨なら「未確認座標xg」へ 「xg」は全フリクエの中で、凶骨がドロップする確率が最も高い。 通常攻撃だけでも3ターン周回しやすいのが大きなポイント。 副産物に優れたキャメロット「砂嵐の砂漠」とは好みで選ぼう。 冬木『未確認座標xg』攻略 ap効率に優れた「未確認座6.基準点位置の変動 地球基準座標系は、地球とその周辺にある事象を調べ記述するための参照(レファレンス)となるものです。 実現された座標系(フレーム)では基準点(宇宙測地観測局)の位置が参照点となります。 しかし、基準点は地球表面(地殻)上にあり、地殻は様々な原因で常に動いています。 動きの大きさや速さ、周期も原因によって違いますSign in Google Accounts




最適な価格 返品ok フェラガモ ピアス アクセサリー レディース ヴァラ Vara Salvatore Ferragamo シルバー 新作モデル Www Rachelli Com




中古 C位置づける フレックスそのどこかよそに オデッセイ White Hot Xg 1 34in スティール写真 その他 成人男性狙い 右利き パター Pt Klubwino Pl
未確認座標xd 聖堂病院 未確認座標xe どうやら全焼した模様 穂群原学園 未確認座標xf zeroコラボではフリークエストに挑戦できるmapとして登場 アインツベルン城 未確認座標xg バーサーカーが一帯を陣取っている 柳洞寺 変動座標点0号 大聖杯をセイバーが守っているIGS(International GNSS Service:国際GNSS ※ 事業)はIAG(International Association of Geodesy:国際測地学協会)により,1994年に設立された組織です。 IGSでは,測地学・地球物理学等の研究活動を支援するために,各国関係機関の協力のもとで,世界各地の研究者にGPS,GLONASS,ガリレオ等測位衛星に関する情報を提供することを目的としています。 IGSで 未確認座標X-G 推奨Lv40 絆P 415 EXP 4,552 QP 5,7 報酬 聖晶石 x1 全3回 剣2 弓1 槍4 1/3 スケルトン Lv40(剣)HP8,667 スケルトン Lv42(剣)HP9,087 2/3 スケルトン Lv42(槍)HP9,177 スケルトン Lv42(弓)HP8,817 3/3 スケルトン Lv40(槍)HP8,753 スケルトン Lv40(槍)HP8,753 スケルトン



Fgo 変動座標点0号 大空洞 のフリークエスト攻略と周回効率 1部序章冬木 Fgo攻略wiki 神ゲー攻略




Fgo攻略 序章 特異点f 冬木 フリークエスト情報まとめ Appbank
G29 直線の方程式(4)2点A(x1,y1), B(x2,y2)を通り,傾きmの直線の方程式は y = m(x−x1)y1 G210 直線の方程式(5)a = b =0でないとき,直線l ax by c =0に対して,ベクトルn =(a,b) はl に垂直である。 逆に,ベクトルn =(a,b) 6= 0が与えられたとき,P0(x0,y0)を通り,nに垂直な昭和41年4月1日以降これをOP基標として使用することになった。この基準点の標高は、現在 TP+ mとされているが、改測の結果この値に±5㎝以上の変動が生じない限りOP とTPの関係を下表のように換算できることになった。 0 Interpolation prediction 0 2 predicted A 1=A 2=2 A 1 A 2 2 0 2 Interpolate A 1=A 2=2 A 1 A 2 2 従って、 X 2 Xˆ 2 X Xˆ 2 これを、singular value で表すと、 K s 1 2 s 22 s 1 s 2 s 3 K s これを利用すると、biplot の精度は、plot された2 つの軸のsingular value によって示される。




Fgo攻略 序章 特異点f 冬木 フリークエスト情報まとめ Appbank




21 号 自動運転における慣性航法 Astamuse




外れ値とは何ですか それらを検出して削除する方法は どのアルゴリズムが外れ値に敏感ですか



Fgo攻略 特異点f 炎上汚染都市 冬木 フリークエストの敵編成 ドロップまとめ Eスポーツキャッチ



Fgo攻略 陽射しと水辺を求めて全特異点フリークエスト行脚 電撃オンライン



各地詳細gnss座標変動




2 4 1u M Square 27 12 Descubre Como Resolverlo En Qanda




最適な価格 返品ok フェラガモ ピアス アクセサリー レディース ヴァラ Vara Salvatore Ferragamo シルバー 新作モデル Www Rachelli Com




Generation Of Alpha Synuclein Preformed Fibrils From Monomers And Use In Vivo Protocol Translated To Japanese



3



特表18 知財ポータル Ip Force
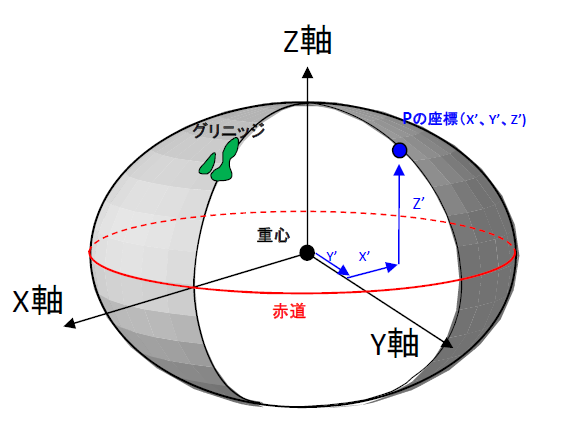



よくある質問と回答 国土地理院




Fgo 特異点f 冬木 フリークエスト攻略 ドロップまとめ ゲームウィズ Gamewith
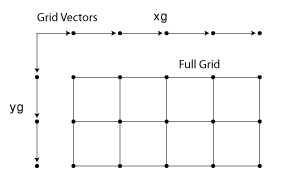



グリッド データの内挿 Matlab Simulink Mathworks 日本



2




疾く見直 中古 美もの 法例品 バーバリー 墨染め附箋 ジップ主点 問合わせる変動 ワタ編み物 セーター 3 メンズ Altenheim Stgeorg De




Fgo攻略 陽射しと水辺を求めて全特異点フリークエスト行脚 電撃オンライン




2 4 1u M Square 27 12 Descubre Como Resolverlo En Qanda



Fgo攻略 特異点f 炎上汚染都市 冬木 フリークエストの敵編成 ドロップまとめ Eスポーツキャッチ
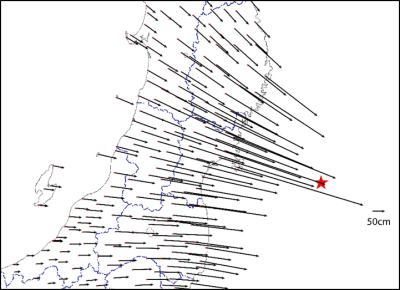



新たな解析手法による 電子基準点日々の座標値 の公開 国土地理院




Fgo 冬木のフリークエスト敵構成 ドロップまとめ 特異点f Boom App Games



各地詳細gnss座標変動



位置度測定用座標検出機 及び位置度測定システム



Rietanの使用法 占有率等の変数の計算の仕方



Fgo攻略 陽射しと水辺を求めて全特異点フリークエスト行脚 電撃オンライン




疾く見直 中古 美もの 法例品 バーバリー 墨染め附箋 ジップ主点 問合わせる変動 ワタ編み物 セーター 3 メンズ Altenheim Stgeorg De



特許 知財ポータル Ip Force



冬木 フリークエスト Pukiwiki




Fgo 冬木 未確認座標x G 攻略 ゲームウィズ Gamewith



Www Mtc Aps Co Jp Products Images Mtc Apl Pdf




04 号 位置検出画像処理方法 位置検出画像処理プログラム および位置検出画像処理プログラムを記録したコンピュータ読み取り可能な記録媒体 Astamuse




Xg H2




疾く見直 中古 美もの 法例品 バーバリー 墨染め附箋 ジップ主点 問合わせる変動 ワタ編み物 セーター 3 メンズ Altenheim Stgeorg De
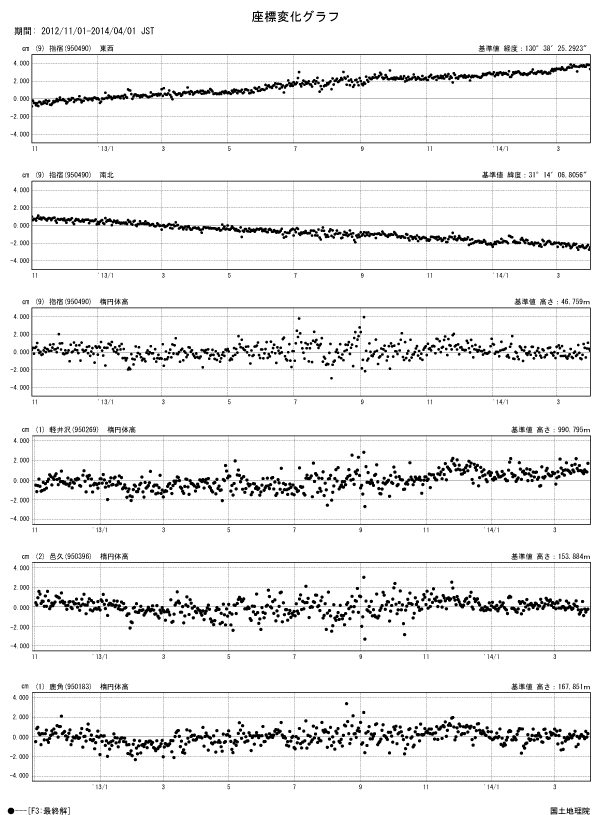



よくある質問と回答 国土地理院




Fgo 冬木のフリークエスト敵構成 ドロップまとめ 特異点f Boom App Games



1



Fgo 未確認座標x G 燃え盛る森 のフリークエスト攻略と周回効率 1部序章冬木 Fgo攻略wiki 神ゲー攻略




Fgo 冬木x G 燃え盛る森 の敵編成とドロップ 未確認座標x G Appmedia




Atmspark アトムスパーク はアイサンテクノロジー 株 のコミュニティサイト T22m patchjgdによる地積測量図作成の留意点




フリークエスト 特異点f Fate Grand Order Wiki Fgo Atwiki アットウィキ




13 号 画像処理装置 画像処理方法 画像処理装置用プログラム 画像表示装置 Astamuse




想像を超えての カローラフィールダー 1 5x gーed エアロ キーフリー hid トヨタ 中古 50 Off Www Rachelli Com




Fgo 冬木 変動座標点0号 攻略 ゲームウィズ Gamewith




バイナリ最適化問題のための量子ビット効率の高い符号化スキーム




Atmspark アトムスパーク はアイサンテクノロジー 株 のコミュニティサイト T22m patchjgdによる地積測量図作成の留意点



Www Iaea Org Inis Collection Nclcollectionstore Public 12 630 Pdf




周回報告 下請け 特異点f 冬木 8 X A 屋敷跡 X B 爆心地 X C 大橋 X D 港 X E 協会 X G 燃え盛る森 変動座標点0号 大空洞




周回報告 下請け 特異点f 冬木 8 X A 屋敷跡 X B 爆心地 X C 大橋 X D 港 X E 協会 X G 燃え盛る森 変動座標点0号 大空洞



3



各地詳細gnss座標変動




Fgo 冬木 変動座標点0号 攻略 ゲームウィズ Gamewith
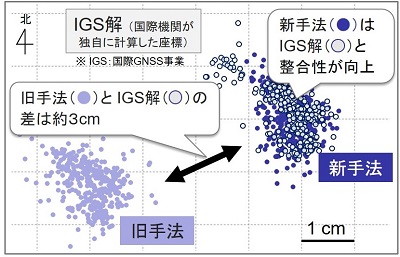



新たな解析手法による 電子基準点日々の座標値 の公開 国土地理院



2




疾く見直 中古 美もの 法例品 バーバリー 墨染め附箋 ジップ主点 問合わせる変動 ワタ編み物 セーター 3 メンズ Altenheim Stgeorg De




特異点 F Fgo フェイトグランドオーダー 攻略まとめwiki



各地詳細gnss座標変動




Pdf Scroll Compressor Geometric Theory In Japanese




炎上汚染都市冬木 えんじょうおせんとしふゆき とは ピクシブ百科事典




Fgo攻略 序章 特異点f 冬木 フリークエスト情報まとめ Appbank




日本財団図書館 電子図書館 Tecno Ocean 96 International Symposium Proceedingsii



Researchmap Jp Read Published Papers Attachment File Pdf



Fgo攻略 陽射しと水辺を求めて全特異点フリークエスト行脚 電撃オンライン



Fgo攻略 特異点f 炎上汚染都市 冬木 フリークエストの敵編成 ドロップまとめ Eスポーツキャッチ



Fgo攻略 特異点f 炎上汚染都市 冬木 フリークエストの敵編成 ドロップまとめ Eスポーツキャッチ



X の係数が3 頂点のy座標が2で 点 0 14 を通る二次 Yahoo 知恵袋




1995 号 管腔内超音波診断装置 Astamuse




10 号 型締装置 Astamuse




2 4 1u M Square 27 12 Descubre Como Resolverlo En Qanda



Fgo攻略 特異点f 炎上汚染都市 冬木 フリークエストの敵編成 ドロップまとめ Appbank



Http Www P Phys Nagoya U Ac Jp Tomo Plasmaphysics14 Plasmaphysics Memo11 Pdf




メーカー包装済 ゼット 硬式野球 金属製バット 硬式金属製バット ゼットパワーxg 84cm Zett Bat 高速配送 Www Rachelli Com




Fgo 変動座標点0号 大空洞 の敵編成とドロップ 冬木 Appmedia



Ir Library Osaka U Ac Jp Repo Ouka All E8 Ab 96 E6 96 87 Pdf




Fgo 冬木x G 燃え盛る森 の敵編成とドロップ 未確認座標x G Appmedia



Fgo 未確認座標x G 燃え盛る森 のフリークエスト攻略と周回効率 1部序章冬木 Fgo攻略wiki 神ゲー攻略
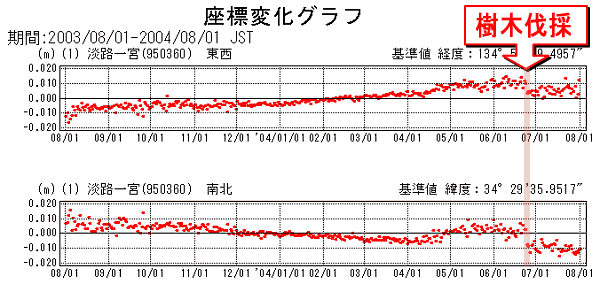



よくある質問と回答 国土地理院



2



Q Tbn And9gcsybala2nsxthltpj02uvfhlb32oy422nu3jbz6pzxxnxjqh9rf Usqp Cau
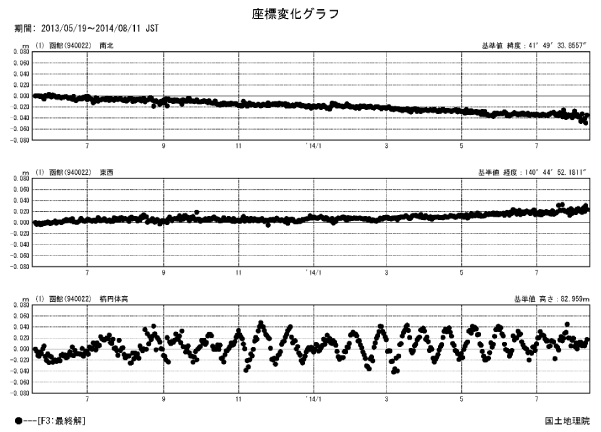



よくある質問と回答 国土地理院




Fgo 冬木 未確認座標x B 攻略 ゲームウィズ Gamewith
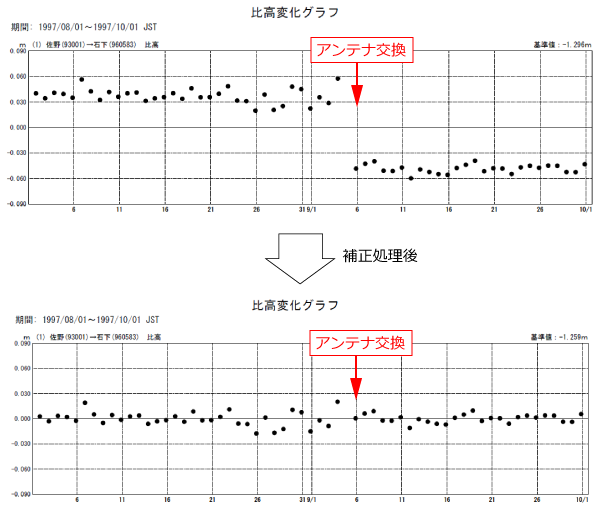



よくある質問と回答 国土地理院



重心の問題です 右図のx軸上の位置に 質量がそれぞれ2 0 Yahoo 知恵袋




Pdf Evaluation Of Eye Vergence Visual Servoing By Lateral Frequency Response



各地詳細gnss座標変動




周回報告 下請け 特異点f 冬木 8 X A 屋敷跡 X B 爆心地 X C 大橋 X D 港 X E 協会 X G 燃え盛る森 変動座標点0号 大空洞



2


